【第1回】
概要と簡単な実装編
本記事では、FFTの概要の説明と、pythonによってテストデータに対して実際にFFT解析を実行します。FFTの基礎を具体例を交えて視覚的に理解できます。
FFT解析の概要
FFT解析とは?
FFT解析という言葉は、エンジニアならだれもが一度は聞いたことはあると思います。そもそもFFTとはFast Fourier Transformの略であり、日本語で言うと、高速フーリエ変換となります。日本語からもわかるように、フーリエ変換を高速で行うものです。では、フーリエ変換とは何か?というところですが、これに関しては基礎の基礎なので大学の教科書に任せるとして、本記事では触れません。「フーリエ変換は時間領域のデータを周波数領域に変換するもの」ぐらいのざっくりした説明でとどめておきたいと思います。
FFTの基礎となる理論
時間領域のデータを周波数領域に変換するための最も基礎となる理論が、(連続時間で定義された)フーリエ変換です。しかし、現実世界での実際のデジタル信号処理では、連続的な信号ではなく、離散的にサンプリングされたデータを扱います。ここで登場するのが離散フーリエ変換、もとい、DFT(Discrete Fourier Transform)**です。
FFTとは、このDFTの計算をアルゴリズムを工夫して計算量を減らして速くしたものであり、数学的にDFTと同じ結果が高速に得られます。
- 連続フーリエ変換:
- 連続時間で定義された最も基礎となる理論
- 離散フーリエ変換(DFT):
- 離散時間で定義されたフーリエ変換
- 高速フーリエ変換(FFT):
- DFTと数学的には同じだが、計算量を減らして高速にしたもの
もう少し詳細を詳しく説明します。
まず、連続時間におけるフーリエ変換は以下の式で定義されます。
ここで:
\[\begin{array}{ll}
x(t) & :時間領域の連続信号\\
X(\omega) & :周波数領域の連続信号 \\
j & :虚数単位
\end{array}
\]
この変換により、時間軸上の連続信号を周波数軸上の連続スペクトルに変換できます。
このフーリエ変換を離散化した、DFTは以下の数式で表されます:
ここで:
\[\begin{array}{ll}
x[n] & :時間領域の離散信号(n = 0, 1, \ldots, N-1) \\
X[k] & :周波数領域の離散信号(k = 0, 1, \ldots, N-1) \\
N & :データ点数 \\
j & :虚数単位
\end{array}
\]
この変換により、時間軸上のN個のデータ点を、周波数軸上のN個の成分に変換できます。この変換をまじめに処理しようとすると、N個のデータに対してO(N2)のオーダーの計算量が必要になります。これを高速に処理できるようなアルゴリズムを使用して、計算を速くしたものがFFTです。計算のオーダーはO(N logN)まで減ります。ただし速く実施したからといって、得られる情報量が減るわけではなく、DFTと数学的に同じ結果が得られるのです。上記からDFTよりもFFTの方が実用的で普及されており、周波数解析することを「FFT解析する」とか「FFTかける」というように現場ではよく言われています。
実例を使ってFFT解析を理解する
では実際にFFT解析をしてどのような結果が得られるのか実例を見ていきましょう。今回はあまりpythonの実装コードには触れず、処理を実行した結果だけ見て内容を理解していただければと思います。詳細は次回の記事にて説明します。
入力信号(時間領域の離散信号)
入力信号は以下の式から得られる時間領域の信号とします。
\[y(t) = a_1 \sin(\omega_1 t) + a_2 \sin(\omega_2 t) + a_3 \sin(\omega_3 t)\]ここで
\[\begin{array}{ll}
a_1 = 3 & :周波数\omega_1の振幅 [\;\;] \\
\omega_1 = 2\pi \times 10 & :10\rm{Hz}の角周波数 \rm{ [rad/s] } \\
a_2 = 1.5 & :周波数\omega_2の振幅 [\;\;] \\
\omega_2 = 2\pi \times 30 & :30\rm{Hz}の角周波数 \rm{ [rad/s] } \\
a_3 = 0.8 & :周波数\omega_3の振幅 [\;\;] \\
\omega_3 = 2\pi \times 60 & :60\rm{Hz}の角周波数 \rm{ [rad/s] } \\
\end{array}
\]
ただし、このy(t)は、連続時間で定義された式であり、これを例えば1000[Hz]のサンプリング周波数で2秒間データを取得したとすると、サンプリングした離散信号は以下となります。
\[y[k] = a_1 \sin(\omega_1 t[k]) + a_2 \sin(\omega_2 t[k]) + a_3 \sin(\omega_3 t[k])\]ここで
\[\begin{array}{ll}
y[k] & :時間領域での離散信号 k=0,1,\ldots,N-1 \\
t[k] = \frac{1}{1000 \rm{[Hz]}} \times k &: 離散時間データ k=0,1,\ldots,N-1 \\
N = 1000 \rm{[Hz]} \times 2\rm{[sec]}=2000 &: データ点数\\
\end{array}
\]
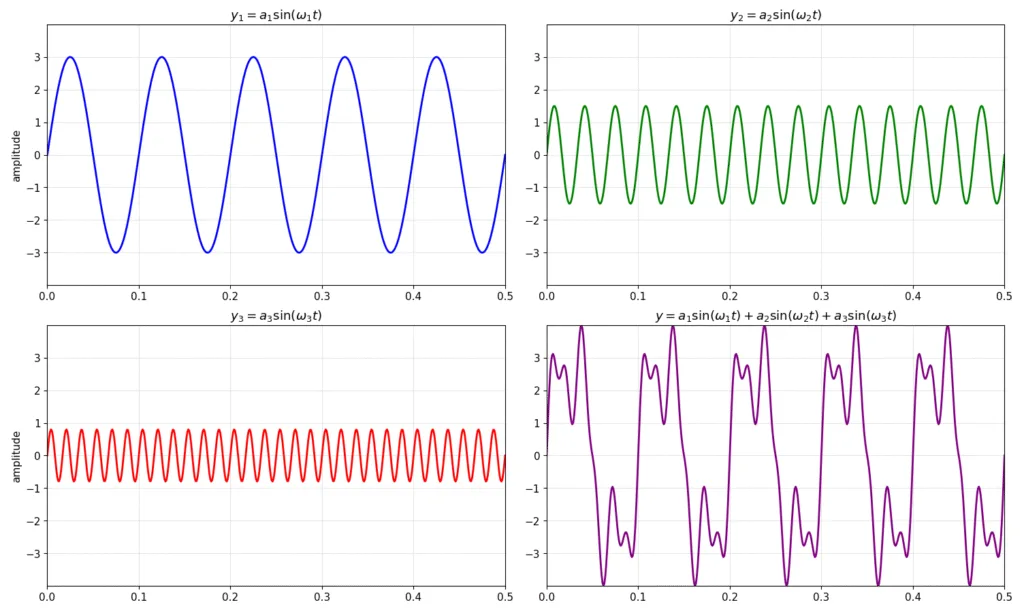
上記y[k]で表される式を、見やすくするために最初の0.5秒間分だけ表示したものが、以下の図の右下の紫のプロットとなります。これが今回FFTをかける対象となるデータです。一見連続信号のように見えますが、拡大すると0.001秒間隔の離散データです。また、今回のy[k]が3つの異なる周波数信号の重ね合わせであり、その1つ1つの元となる信号も今回プロットしました。左上の青プロットが、振幅3、周波数10Hzの信号、右上の緑のプロットが、振幅1.5、周波数30HZのプロット、左下の赤のプロットが、振幅0.8、周波数60Hzのプロットです。
FFT解析の結果(周波数領域の離散信号)
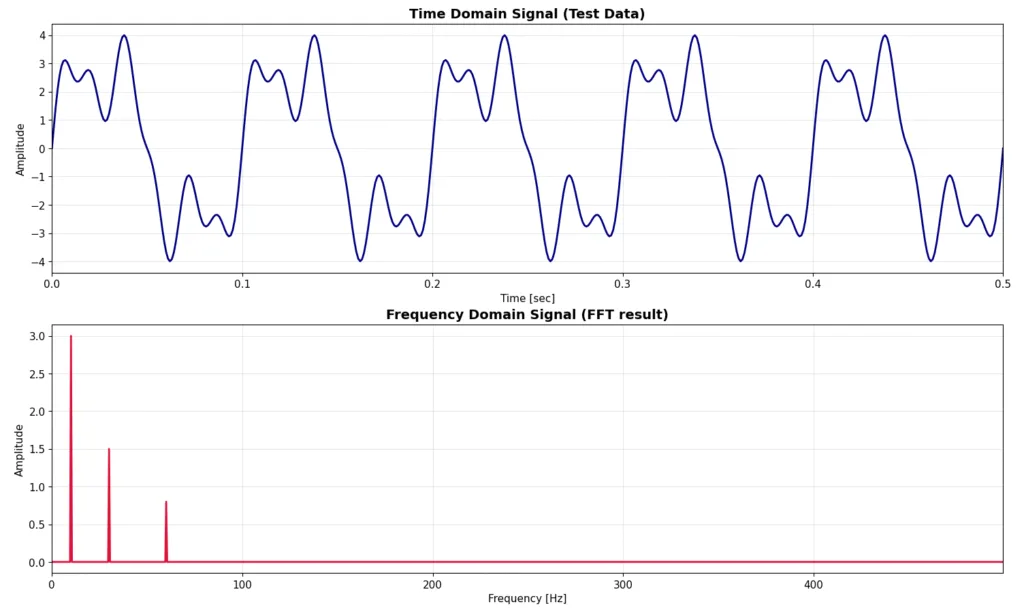
先ほど生成した時間領域の離散信号y[k]に対して、FFT解析を実施した結果が、以下の図の下のプロットになります。上のプロットはy[k]を改めて最初の0.5秒の部分をプロットしたものになります。下の赤のプロットは横軸が周波数 [Hz]、縦軸が振幅 [ ]です。横軸の補助線が100Hz単位なのでわかりにくいかもしれませんが、10Hzのところに振幅3のピーク、30Hzのところに振幅1.5のピーク、60Hzのところに振幅0.8のピークがたっていることがわかります。これがFFT解析の最も基本的な出力です。意味としては、FFT解析の入力の時間領域の信号には、10, 30, 60 Hzの周波数の信号が、それぞれ3.0, 1.5, 0.8の振幅で含まれているという意味です。まさに、元となったy(t)の式と同じ意味を表しています。時間領域の信号だけ見ていると(下図青のプロット)規則性も良くわからなかったものが、FFTをかけて周波数領域で見ることでシンプルな3つの周波数の信号だけで成り立っているということがわかりました。これがFFT解析です。
Python実装を確認する
先ほどの実例で示した、FFT解析を実施するためのPythonコードを以下に示します。詳細の説明は次回に回したいと思います。
メインプログラム(main.py)
メインプログラムはこちらです。メインプログラムが煩雑になるのを防ぐため、機能ごとに関数化して、FFT_libというファイルにまとめ、それをインポートする形としています。
import numpy as np
import FFT_lib as fft
# サンプリング設定
sampling_rate = 1000 # 1000Hz(1秒に1000回測定)
duration = 2.0 # 2秒間
N = int(sampling_rate * duration) # 総サンプル数
# 時間軸を作成
t = np.linspace(0, duration, N, endpoint=False)
# サンプルデータの周波数と振幅を設定
freq1, freq2, freq3 = 10, 30, 60 # Hz
amp1, amp2, amp3 = 3.0, 1.5, 0.8 # 振幅
# 3つの周波数が混合した信号を生成
signal1, signal2, signal3, mixed_signal = fft.generate_testData(t, freq1, freq2, freq3, amp1, amp2, amp3)
print(f"テストデータが作成されました:y(t) = {amp1}*sin(2π{freq1}t) + {amp2}*sin(2π{freq2}t) + {amp3}*sin(2π{freq3}t)")
# 生成した信号をプロット
t_short = 0.5 # 最初の0.5秒だけ表示
fft.plot_testData(t, 0.5, signal1, signal2, signal3, mixed_signal)
print("時間領域での信号をプロットしました。")
# FFT解析を実行
frequency, amplitude, fft_result = fft.execute_fft(mixed_signal, sampling_rate)
print("FFT解析を実行しました。")
print(f"周波数分解能: {frequency[1] - frequency[0]:.2f} Hz")
print(f"最大周波数: {frequency[-1]:.0f} Hz (ナイキスト周波数)")
# FFT解析の結果をプロット
fft.plot_fftResult(t, t_short, mixed_signal, frequency, amplitude)
関数ファイル(FFT_lib.py)
こちらは関数ファイルです。メインプログラムに使用される機能を関数化してまとめています。
import numpy as np
import matplotlib.pyplot as plt
from scipy.fft import fft, fftfreq
# グラフを美しくする設定
plt.rcParams['figure.figsize'] = (12, 8)
plt.rcParams['font.size'] = 11
# 3つの周波数が混合した信号を生成
def generate_testData(t,freq1,freq2,freq3,amp1,amp2,amp3):
"""3つの周波数が混合した信号を生成
Takes :
t: 時間軸 [sec]
freq1, freq2, freq3: 周波数1, 2, 3 [Hz]
amp1, amp2, amp3: 振幅1, 2, 3 [ ]
Returns:
signal1, signal2, signal3: 個別の正弦波信号 [ ]
mixed_signal: 3つの信号を混合したもの [ ]
"""
signal1 = amp1 * np.sin(2 * np.pi * freq1 * t)
signal2 = amp2 * np.sin(2 * np.pi * freq2 * t)
signal3 = amp3 * np.sin(2 * np.pi * freq3 * t)
# 3つの信号を混合
mixed_signal = signal1 + signal2 + signal3
return signal1, signal2, signal3, mixed_signal
def plot_testData(t, t_short, signal1, signal2, signal3, mixed_signal):
"""時間域での信号をプロット
Takes : t: 時間軸
t_short: 最初の何秒間を表示するか
signal1, signal2, signal3: 個別の正弦波信号
mixed: 3つの信号を混合したもの
Returns: None
"""
fig, axes = plt.subplots(2, 2, figsize=(15, 10))
mask = t <= t_short
t_short_list = t[mask]
# 縦軸範囲を全プロットで統一
y_min = min(signal1[mask].min(), signal2[mask].min(), signal3[mask].min(), mixed_signal[mask].min())
y_max = max(signal1[mask].max(), signal2[mask].max(), signal3[mask].max(), mixed_signal[mask].max())
# 個別信号
axes[0, 0].plot(t_short_list, signal1[mask], 'b-', linewidth=2, label='10Hz')
axes[0, 0].set_title(r'$y_1 = a_1 \sin(\omega_1 t)$', fontweight='bold')
axes[0, 0].grid(True, alpha=0.3)
axes[0, 0].set_ylabel('amplitude')
axes[0, 0].set_xlim(0, t_short)
axes[0, 0].set_ylim(y_min, y_max)
axes[0, 1].plot(t_short_list, signal2[mask], 'g-', linewidth=2, label='30Hz')
axes[0, 1].set_title(r'$y_2 = a_2 \sin(\omega_2 t)$', fontweight='bold')
axes[0, 1].grid(True, alpha=0.3)
axes[0, 1].set_xlim(0, t_short)
axes[0, 1].set_ylim(y_min, y_max)
axes[1, 0].plot(t_short_list, signal3[mask], 'r-', linewidth=2, label='60Hz')
axes[1, 0].set_title(r'$y_3 = a_3 \sin(\omega_3 t)$', fontweight='bold')
axes[1, 0].grid(True, alpha=0.3)
axes[1, 0].set_ylabel('amplitude')
axes[1, 0].set_xlim(0, t_short)
axes[1, 0].set_ylim(y_min, y_max)
# 混合信号
axes[1, 1].plot(t_short_list, mixed_signal[mask], 'purple', linewidth=2)
axes[1, 1].set_title(r'$y = a_1 \sin(\omega_1 t) + a_2 \sin(\omega_2 t) + a_3 \sin(\omega_3 t)$', fontweight='bold')
axes[1, 1].grid(True, alpha=0.3)
axes[1, 1].set_xlim(0, t_short)
axes[1, 1].set_ylim(y_min, y_max)
plt.tight_layout()
plt.show()
def execute_fft(mixed_signal, sampling_rate):
"""信号にFFTを適用して周波数解析
Takes : signal: 入力信号 [ ]
sampling_rate: サンプリング周波数 [Hz]
Returns: frequencies_positive: 正の周波数成分 [Hz]
amplitude_single_sided: 片側振幅スペクトラム [ ]
fft_result: FFTの複素数結果 [ ]
"""
N = len(mixed_signal)
# FFT実行
fft_result = fft(mixed_signal)
# 周波数軸を作成
frequencies = fftfreq(N, 1 / sampling_rate)
# 振幅スペクトラムを計算(複素数の絶対値)
amplitude_spectrum = np.abs(fft_result)
# 正の周波数のみ取得(実信号の場合、負の周波数は冗長)
positive_freq_mask = frequencies >= 0 # DC成分(0Hz)も含む
frequencies_positive = frequencies[positive_freq_mask]
amplitude_positive = amplitude_spectrum[positive_freq_mask]
# 片側振幅スペクトラムに変換(DC成分以外は2倍)
amplitude_single_sided = amplitude_positive * 2 / N
amplitude_single_sided[0] = amplitude_positive[0] / N # DC成分のみ2倍しない
return frequencies_positive, amplitude_single_sided, fft_result
def plot_fftResult(t, t_short, mixed_signal, frequency, amplitude):
"""FFT結果を美しく可視化(片側振幅スペクトラム)"""
fig, (ax1, ax2) = plt.subplots(2, 1, figsize=(14, 10))
# 上段:時間領域
time_mask = t <= t_short
ax1.plot(t[time_mask], mixed_signal[time_mask], 'navy', linewidth=2)
ax1.set_title('Time Domain Signal (Test Data)', fontsize=14,fontweight='bold')
ax1.set_xlabel('Time [sec]')
ax1.set_ylabel('Amplitude')
ax1.set_xlim(0, t_short)
ax1.grid(True, alpha=0.3)
# 下段:周波数領域
ax2.plot(frequency, amplitude, 'crimson', linewidth=2)
ax2.set_title('Frequency Domain Signal (FFT result)', fontsize=14, fontweight='bold')
ax2.set_xlabel('Frequency [Hz]')
ax2.set_ylabel('Amplitude')
ax2.set_xlim(0, frequency[-1])
ax2.grid(True, alpha=0.3)
plt.tight_layout()
plt.show()次回予告
次回は、Pythonコードの内容を細かく説明します。





コメント
コメント一覧 (1件)
Hi, this is a comment.
To get started with moderating, editing, and deleting comments, please visit the Comments screen in the dashboard.
Commenter avatars come from Gravatar.