【第5回】
スペクトル漏れと窓関数(Spectral leakage & window function)
本記事ではFFTにおけるスペクトル漏れ(Spectral leakage)と、その対策としての窓関数(window function)について説明します。本記事を読むことで、FFTを実施した際に発生するスペクトル漏れという現象を正しく理解し、またそれに対する対策として窓関数の適用について理解することができます。今回は窓関数はハニング関数(Hanning window)とし、実際にテストデータを使用して、適宜視覚化してその挙動を説明します。
現実世界における周波数解析は、測定対称の正確な周波数がわからないことが多く(それを知るために周波数解析をするのだから)、測定の際のサンプリング周波数やサンプリング時間は、必ずしも測定対象の周波数に対して最適ではありません。そのような場合に真の周波数成分の周辺に疑似的な周波数成分が漏れ出てくる現象が、「スペクトル漏れ」と呼ばれる現象です。この現象を正しく理解し、FFTの結果に振り回されることなく正しく判断するということが、エンジニアに求められるスキルです。
本記事を読む前に概要(こちら)と実践編(こちら)の記事を読むことを推奨します。
スペクトル漏れが発生するメカニズム
テストデータの説明
今回のテストデータは以下で表される信号を、500Hzで2秒間サンプリングした離散信号とします。
\[y(t) = a_1 \sin\omega_1 t + a_2 \sin\omega_2 t\]ここで
\[\begin{array}{ll}
a_1 = 3 & :周波数\omega_1の振幅 [\;\;] \\
\omega_1 = 2\pi \times 6.3 & :6.3\rm{Hz}の角周波数 \rm{ [rad/s] } \\
a_2 = 1.5 & :周波数\omega_2の振幅 [\;\;] \\
\omega_2 = 2\pi \times 25 & :25\rm{Hz}の角周波数 \rm{ [rad/s] } \\
\end{array}
\]
となります。
言葉でこのテストデータの説明をすると、この信号は振幅3の6.3Hzの正弦波と、振幅1.5の25Hzの正弦波の重ね合わせとなります。
テストデータの視覚化
上記テストデータをプロットしたものが以下の図1となります。
- 左上:振幅3、周波数6.3Hzの正弦波成分のプロット
- 右上:振幅1.5、周波数25Hzの正弦波成分のプロット
- 左下:窓関数(Hanning window)のプロット
- 右下:正弦波成分の重ね合わせのプロット(紫)と、それに窓関数をかけあわせたプロット(オレンジ)
左下の窓関数に関しては後程詳しく説明します。
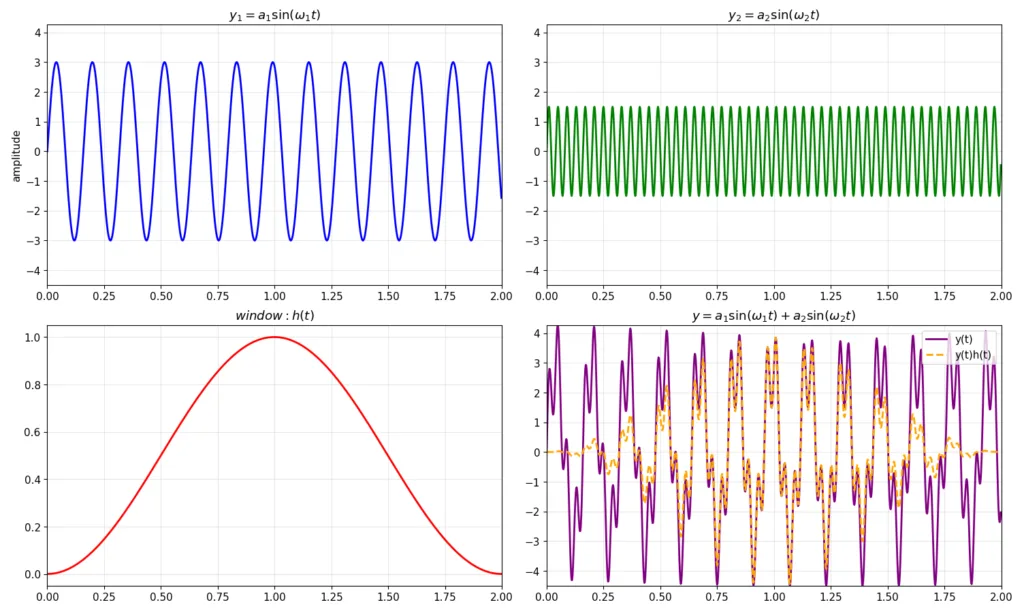
図1:テストデータと窓関数のプロット
スペクトル漏れの現象の視覚化
テストデータにFFTを適用すると、得られる結果は以下の図2のようになります。図1の右下の紫のプロットをFFTしたものになります。そして図3が、図2の周波数プロットの、低周波部分を拡大したものになります。
25Hz周辺は想定通り、25Hzに1点だけピークがたっていますが、6.3Hzの周辺はある程度広がりを持った結果が得られています。この6.3Hz周辺に発生している現象がスペクトル漏れ(Spectral leakage)という現象です。
ここで重要なのが、テストデータには6.3Hzと25Hzしか含まれていないはずなのに、FFTを適用すると、6.3Hzと25Hzのみにピークがたつわけではなく、6.0Hzや6.5Hzやその先の周波数成分が含まれた結果が得られてしまうという点です。実験でFFT解析を実施する際は、この点に気を付けて結果を見るようにしてください。
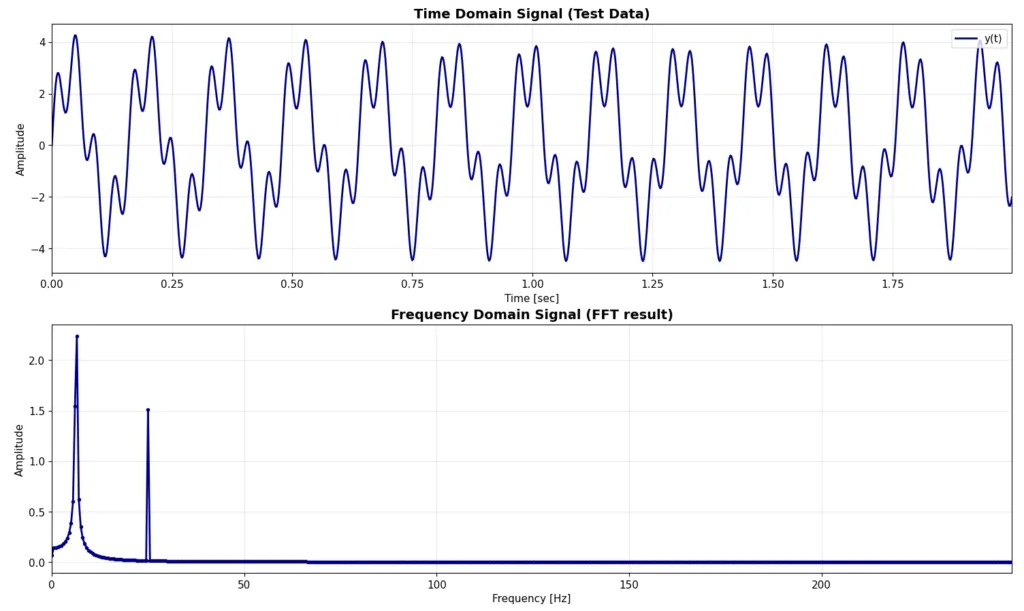
図2:テストデータのFFTの結果(窓関数の適用なし)
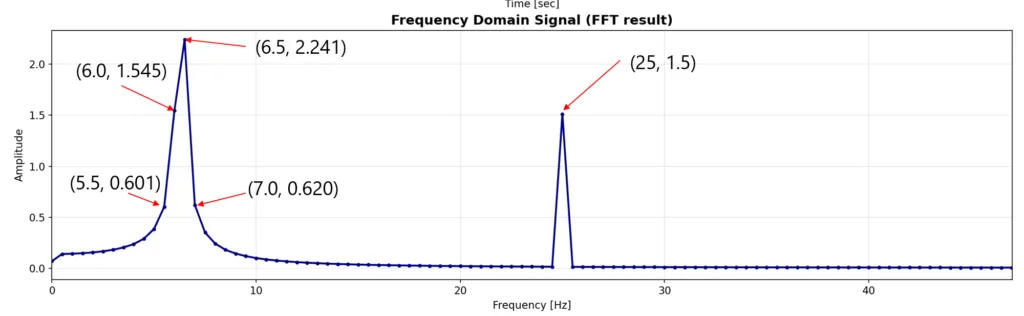
図3:周波数領域の拡大
スペクトル漏れのメカニズム
上記の結果からスペクトル漏れ(Spectral leakage)がどのような現象なのかは理解できたと思います。次はなぜスペクトル漏れが発生するのか、また6.3Hzの信号に対してはスペクトル漏れが発生したのに、25Hzの信号に対してはスペクトル漏れが発生しなかった理由を説明します。
スペクトル漏れが発生する理由を簡単に言うと、「時間領域データの中に、その周波数成分の信号がぴったりの周期で収まっていない」ことが原因です。FFT(及びDFT)は、「元データとしている有限時間の離散信号が、無限に繰り返される」という前提でのアルゴリズムとなっているためです。つまりFFTの対象となっている元データに、1周期の整数倍の長さのデータがぴったり収まっている周波数成分はスペクトル漏れが発生せず、逆に、元データに1周期の整数倍の長さのデータがぴったり収まっていない周波数成分はスペクトル漏れが発生します。以下の図4、図5にスペクトル漏れが発生するパターン、しないパターンを図示しました。元データに1周期の整数倍の長さのデータが入っていない場合、それが無限に繰り返されるとすると、継ぎ目に中途半端な部分が必ず発生し、正確な正弦波ではなくなってしまいます(図5の赤線部)。この部分がスペクトル漏れを発生させる要因です。
今回のテストデータでいうと、1つ目の周波数成分が6.3Hzという中途半端な周波数で、図1の左上のプロットを見てもらえたらわかりますが、2秒間のデータに6.3Hzの正弦波が、ぴったり整数倍周期分ではなく、中途半端なところで終わっていることがわかります。6.3Hzなので、2秒間だと、6.3×2 = 12.6回分の振動が収まってることとなり、整数回ではないことからも明らかです。逆に、25Hzの方は、2秒間の間に、25×2 = 50回分の振動が収まっており、ぴったり整数回の周期が収まっています。その結果図4のような正確な正弦波に対するFFTが実施され、スペクトル漏れが出ないという仕組みになっています。
また、周波数分解能の観点からも説明できます。FFT(DFT)は、離散フーリエ変換であり、離散的な周波数成分に対する結果しか得られません。今回のテストデータは、2秒間の信号なので、周波数分解能は0.5Hzであり、0.5Hz刻みの周波数成分しか表示できません(FFTにおける周波数分解能はこちらで説明しています)。一方で、解析対象の周波数は6.3Hzと25Hzで、6.3Hzの方は0.5Hz刻みだとスキップしてしまうため、正確な値が得られません。
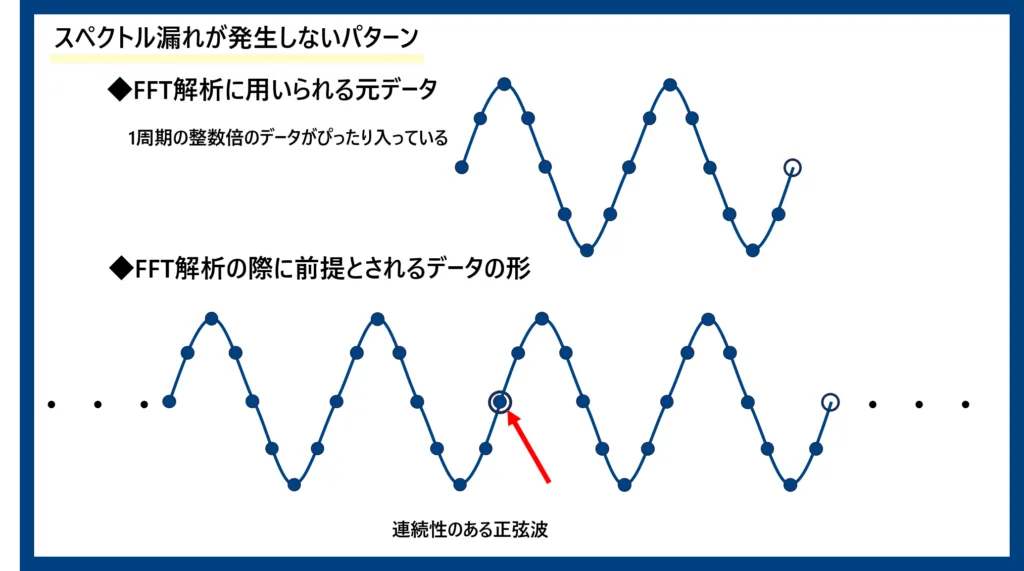
図4:スペクトル漏れが発生しないパターン
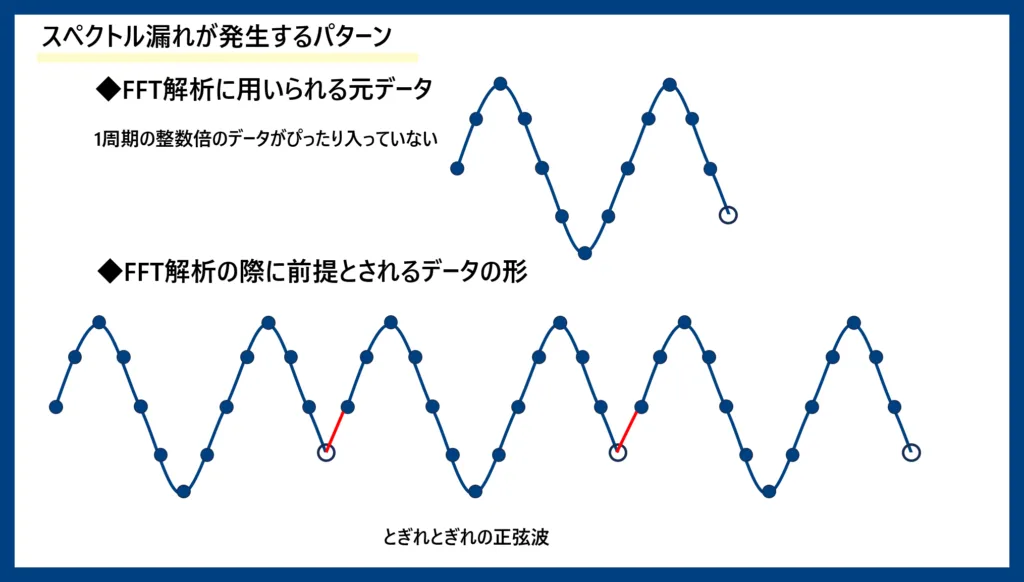
図5:スペクトル漏れが発生するパターン
数式での確認は今回は省略しますが、以下のDFTの式にy[n] ( = y(n*Δt) )を代入して確認すれば、スペクトル漏れが発生するパターンと発生しないパターンがわかると思います。(計算は少し大変ですが)
\[Y[k] = \sum_{n=0}^{N-1} y[n] \cdot \exp\left(-j\frac{2\pi kn}{N}\right)\]窓関数によるスペクトル漏れの低減の確認
窓関数の概要
上記の「スペクトル漏れ」に対する対策方法として窓関数を適用する、という方法があります。ここで注意してほしいこととして、窓関数を適用して得られる効果は、「スペクトル漏れがなくなる」のではなく、「スペクトル漏れが軽減する」です。スペクトル漏れは、元データに中途半端な周期の周波数成分が含まれてしまっている時点で回避することは不可能で、せいぜい窓関数を適用してその影響を軽減することができる程度です。さらに、窓関数を適用することには副作用もあり、実質の周波数分解能が下がったり、振幅が小さく得られたりします。なので、窓関数を適用することのメリットデメリットをしっかり理解することが重要です。
窓関数を適用することは、以下のメリットデメリットがあることを認識してください。
- メリット:
- スペクトル漏れの影響を小さくでき、ピーク周波数がわかりやすくなる
- デメリット:
- 周波数分解能が小さくなる
- 振幅が減衰してしまう
窓関数の効果確認
では窓関数を適用した場合のFFT解析への影響をテストデータで確認しましょう。今回は窓関数としてハニング関数を用います。窓関数には、他にも矩形・はみ窓関数を適用した場合のFFT解析への影響をテストデータで確認しましょう。今回は窓関数としてハニング関数を用います。窓関数には、代表的なものとしては、矩形窓・ハン関数(ハニング窓関数)・ハミング関数という3種類のものがあります。役割、効果としては3つとも大きな差はないので今回はよく使われるハニング関数を使用します。
(Hann windowは数式では以下のように表されます。
\[h[n]
= \frac{1}{2}
\left(
1 – \cos\!\left(\frac{2\pi n}{N-1}\right)
\right),
\quad n = 0,1,\dots,N-1
\]
図1の左下の赤のプロットが上記ハニング窓関数のプロットです。プロットからも数式からもわかるように、データの両端点が0になっています。このハニング窓関数を元データに掛け合わせたものが図1の右下のオレンジのプロットです。ハニング窓関数をかけることで、有限時間のデータセットの両端が強制的に0になり、図5で示したような、データの継ぎ目に発生する、不連続性が軽減されます(両端が0なので)。これによって、スペクトル漏れが軽減する、という効果が得られます。軽減!です。なくなるわけではありません。
以下の図6にハニング窓関数の適用有り無しのFFT結果の比較を示しました。そして図7に低周波部分の結果の拡大図を載せました。見てもらうとわかるように、6.3Hz周辺のスペクトル漏れは、窓関数を適用することで軽減され、ピークがスリムになっていることがわかると思います。一方で25Hzの方は、逆にピークが太ってしまう結果となっています。これは、25HzはFFT(DFT)の周波数分解能的にスペクトル漏れが発生しなかった周波数であり、ハニング窓関数を適用したことで、逆にぴったりの周波数からスペクトルが漏れ出してしまったために起こっています。また、6.3Hz,、25Hzのピークを見てもらうとわかるように、窓関数の適用がないときに比べ、振幅が半分になっていることがわかります。これが窓関数を利用する際の副作用になるので注意してください。ハニング窓関数では振幅は、約0.5倍になります。理由が気になる方は、”コヒーレントゲイン”とかで調べてみてください。本記事では本筋から外れるので言及しないことにします。
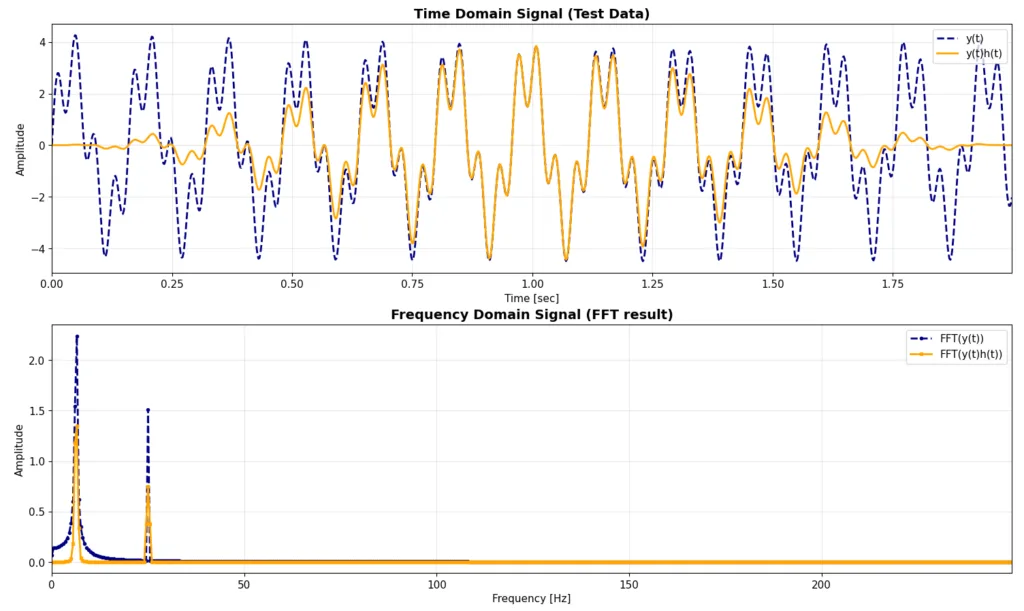
図6:テストデータのFFTの結果(窓関数の適用あり)
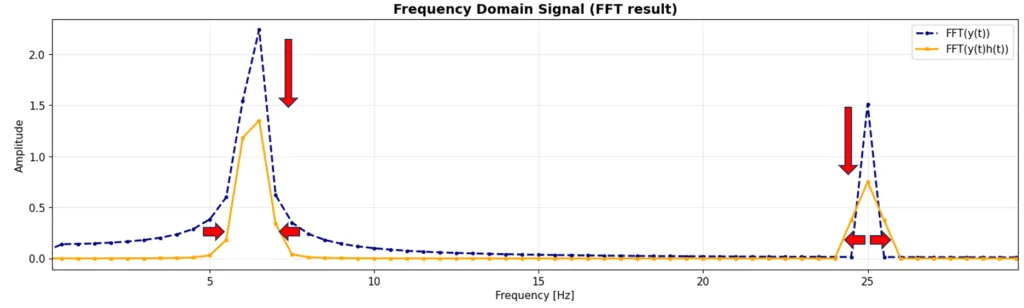
図7:周波数領域の拡大
Tips:乗算と畳み込み積分(convolution)の関係
ここでTipsとして、乗算と畳み込み積分の関係を簡単説明して、今回の例を参考に実例を確認してみましょう。本筋とは外れる内容なので、興味がない人は読み飛ばしてください。
今回のテストデータy(t)と窓関数h(t)を掛け合わせたものは、周波数領域ではそれぞれのフーリエ変換のY(ω)とH(ω)の畳み込み積分になります。連続時間では以下のような式になります。
\[y(t)\, h(t)
\;\longleftrightarrow\;
\frac{1}{2\pi}
\int_{-\infty}^{\infty}
Y(\omega-\Omega)\, H(\Omega)\, d\Omega
\]
離散時間において、有限長さのデータy[n]とh[n]に対して、FFTの結果のY[k], H[k]もそれぞれ有限長さになってしまうので、単純な畳み込み積分ではなく、循環畳み込み積分を使用します(両端部分を、無限に同じデータセットが繰り返されているという前提で畳み込み積分を行う方法)。循環畳み込み積分の詳細は教科書にお任せします。この離散時間における関係は以下の式で表されます。
\[y[n]\, h[n]
\;\longleftrightarrow\;
\frac{1}{N}
\sum_{m=0}^{N-1}
Y[m]\,
H[(k-m)\!\!\mod N]
\]
mod Nが入っているのは、循環畳み込み積分の特徴ですね。
では実際に今回のテストデータへの適用事例を確認してみましょう。以下の図8の上のプロットを説明します。水色|FFT(signal * window)|は、y[n]h[n]を時間領域で掛け算してから、FFTをかけた結果です。そして重なっているオレンジの点線のプロットが、y[n]、h[n]をそれぞれ個別のFFTをかけてえられたY[k]とH[k]を畳み込み積分で計算した結果です。ぴったり同じ結果になっていることがわかると思います。図8の下のプロットはy[n], h[n]をそれぞれ個別にFFTした結果です。青のプロットがY[k]、緑のプロットがH[k]です。青のプロットY[k]を固定して、緑のプロットH[k]を1つずつ右にずらしていって、その時のY[k]とH[k]の各点の掛け算を足し合わせるというのを、ひたすら繰り返していくと、オレンジの結果が得られます。先に説明した、ぴったりの周波数のピークが太る理由もこれでわかりやすいかと思います。
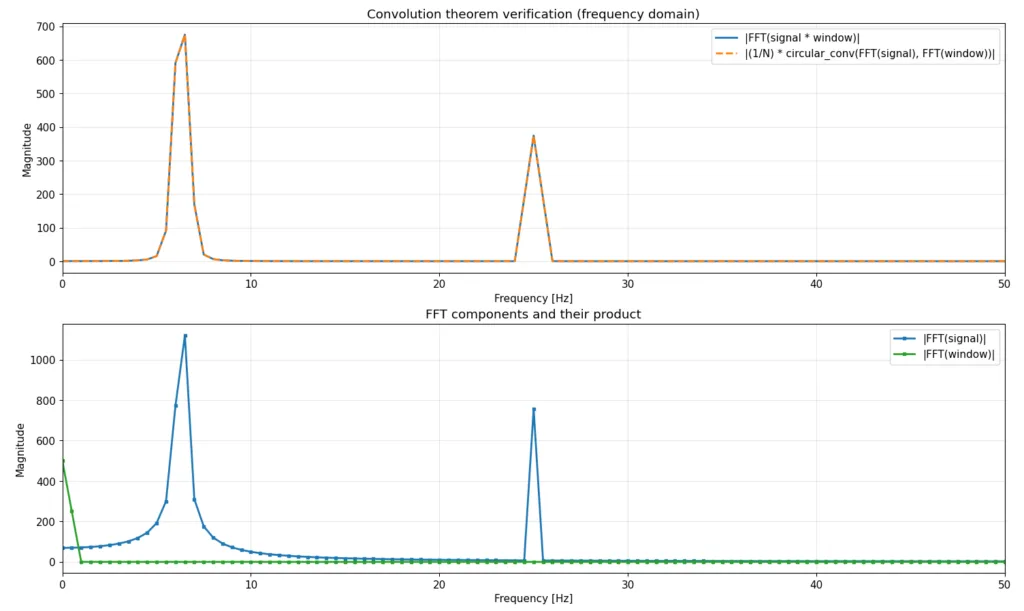
図8:乗算と畳み込み積分の関係
pythonコードの確認
メインプログラム(main.py)
こちらがメインプログラムです。実装内容は前回からあまり変わっていないので特に説明は不要かと思います。58行目以降はTipsの内容なので不要な人は削除してください。
```python
import numpy as np
import FFT_lib as fft
# サンプリング設定
sampling_rate = 500 # 500Hz(1秒に500回測定)
duration = 2.0 # 2秒間
N = int(sampling_rate * duration) # 総サンプル数
# 時間軸を作成
t = np.linspace(0, duration, N, endpoint=False)
# サンプルデータの周波数と振幅を設定
freq1, freq2 = 6.3, 25 # Hz
amp1, amp2 = 3.0, 1.5 # 振幅
# 2つの周波数が混合した信号を生成
signal1, signal2, mixed_signal = fft.generate_testData(t, freq1, freq2, amp1, amp2)
print(f"テストデータが作成されました:y(t) = {amp1}*sin(2π{freq1}t) + {amp2}*sin(2π{freq2}t))")
# 窓関数を生成
window = fft.generate_hanning_window(N)
# 生成した信号に窓関数を適用
mixed_signal_window = fft.apply_window(mixed_signal, window)
# 生成した信号と窓関数をプロット
t_short = 2.0 # 最初の2.0秒だけ表示
fft.plot_testData(t, 2.0, signal1, signal2, mixed_signal, window, mixed_signal_window)
print("時間領域での信号をプロットしました。")
# 窓関数がない場合のFFT解析を実行
frequency, amplitude, fft_result = fft.execute_fft(mixed_signal, sampling_rate)
print("FFT解析を実行しました。")
print(f"周波数分解能: {frequency[1] - frequency[0]:.2f} Hz")
print(f"最大周波数: {frequency[-1]:.0f} Hz (ナイキスト周波数)")
# FFT解析の結果をプロット
fft.plot_fftResult(t, mixed_signal, frequency, amplitude)
# 窓関数をかけた場合のFFT解析を実行
frequency_window, amplitude_window, fft_result_window = fft.execute_fft(
mixed_signal_window, sampling_rate
)
# FFT解析の結果をプロット(窓あり・なしを比較)
fft.plot_fftResult_window(
t,
mixed_signal,
mixed_signal_window,
frequency,
amplitude,
frequency_window,
amplitude_window
)
print("窓適用後の FFT をプロットしました。")
# === 畳み込み定理の検証 ===
freqs, Y_windowed, conv_scaled, X, H = fft.verify_convolution_theorem(mixed_signal, window, sampling_rate)
# 誤差の簡易評価
abs_diff = np.max(np.abs(Y_windowed - conv_scaled))
rel_diff = abs_diff / (np.max(np.abs(Y_windowed)) + 1e-12)
print(f"最大絶対差 (FFT(windowed) vs (1/N)*circular_conv): {abs_diff:.3e}")
print(f"相対差(最大振幅比): {rel_diff:.3e}")
# 比較プロット
fft.plot_convolution_verification(freqs, Y_windowed, conv_scaled, X, H, sampling_rate, show_phase=False)
print("畳み込み定理の検証プロットを表示しました。")
```
関数ファイル(FFT_lib.py)
94行目を見るとわかりますが、numpyに便利なnp.hanning(*)というものがあり、データ長さだけ指定すれば、ハニング窓関数を生成してくれます。
```python
import numpy as np
import matplotlib.pyplot as plt
from scipy.fft import fft, fftfreq, ifft
# グラフを美しくする設定
plt.rcParams['figure.figsize'] = (12, 8)
plt.rcParams['font.size'] = 11
# 3つの周波数が混合した信号を生成
def generate_testData(t, freq1, freq2, amp1, amp2):
"""3つの周波数が混合した信号を生成
Takes :
t: 時間軸 [sec]
freq1, freq2, freq3: 周波数1, 2, 3 [Hz]
amp1, amp2, amp3: 振幅1, 2, 3 [ ]
Returns:
signal1, signal2, signal3: 個別の正弦波信号 [ ]
mixed_signal: 3つの信号を混合したもの [ ]
"""
signal1 = amp1 * np.sin(2 * np.pi * freq1 * t)
signal2 = amp2 * np.sin(2 * np.pi * freq2 * t)
# 3つの信号を混合
mixed_signal = signal1 + signal2
return signal1, signal2, mixed_signal
def plot_testData(t, t_short, signal1, signal2, mixed_signal, window, mixed_signal_window):
"""時間域での信号をプロット"""
fig, axes = plt.subplots(2, 2, figsize=(15, 10))
mask = t <= t_short
t_short_list = t[mask]
# 縦軸範囲を全プロットで統一
y_min = min(signal1[mask].min(), signal2[mask].min(),
mixed_signal[mask].min(), mixed_signal_window[mask].min())
y_max = max(signal1[mask].max(), signal2[mask].max(),
mixed_signal[mask].max(), mixed_signal_window[mask].max())
axes[0, 0].plot(t_short_list, signal1[mask], 'b-', linewidth=2)
axes[0, 0].set_title(r'$y_1 = a_1 \sin(\omega_1 t)$', fontweight='bold')
axes[0, 0].grid(True, alpha=0.3)
axes[0, 0].set_xlim(0, t_short)
axes[0, 0].set_ylim(y_min, y_max)
axes[0, 1].plot(t_short_list, signal2[mask], 'g-', linewidth=2)
axes[0, 1].set_title(r'$y_2 = a_2 \sin(\omega_2 t)$', fontweight='bold')
axes[0, 1].grid(True, alpha=0.3)
axes[0, 1].set_xlim(0, t_short)
axes[0, 1].set_ylim(y_min, y_max)
axes[1, 0].plot(t, window, 'r-', linewidth=2)
axes[1, 0].set_title(r'$window: h(t)$', fontweight='bold')
axes[1, 0].grid(True, alpha=0.3)
axes[1, 0].set_xlim(0, t_short)
axes[1, 1].plot(t_short_list, mixed_signal[mask], 'purple', linewidth=2, label='y(t)')
axes[1, 1].plot(t_short_list, mixed_signal_window[mask],
color='orange', linestyle='--', linewidth=2, label='y(t)h(t)')
axes[1, 1].set_title(r'$y = a_1 \sin(\omega_1 t) + a_2 \sin(\omega_2 t)$',
fontweight='bold')
axes[1, 1].grid(True, alpha=0.3)
axes[1, 1].set_xlim(0, t_short)
axes[1, 1].set_ylim(y_min, y_max)
axes[1, 1].legend()
plt.tight_layout()
plt.show()
def execute_fft(mixed_signal, sampling_rate):
"""信号にFFTを適用して周波数解析"""
N = len(mixed_signal)
fft_result = fft(mixed_signal)
frequencies = fftfreq(N, 1 / sampling_rate)
amplitude_spectrum = np.abs(fft_result)
pos_mask = frequencies >= 0
frequencies_positive = frequencies[pos_mask]
amplitude_positive = amplitude_spectrum[pos_mask]
amplitude_single_sided = amplitude_positive * 2 / N
amplitude_single_sided[0] = amplitude_positive[0] / N
return frequencies_positive, amplitude_single_sided, fft_result
def generate_hanning_window(N):
"""ハニング窓を生成"""
return np.hanning(N)
def apply_window(signal, window):
"""窓を信号に適用"""
if len(signal) != len(window):
raise ValueError("signal and window must have the same length")
return signal * window
def plot_fftResult(t, mixed_signal, frequency, amplitude):
"""FFT結果を可視化"""
fig, (ax1, ax2) = plt.subplots(2, 1, figsize=(14, 10))
ax1.plot(t, mixed_signal, 'navy', linewidth=2)
ax1.set_title('Time Domain Signal', fontweight='bold')
ax1.grid(True, alpha=0.3)
ax2.plot(frequency, amplitude, 'navy', linewidth=2, marker='o', markersize=3)
ax2.set_title('Frequency Domain Signal', fontweight='bold')
ax2.grid(True, alpha=0.3)
plt.tight_layout()
plt.show()
def plot_fftResult_window(t, mixed_signal, mixed_signal_window,
frequency, amplitude,
frequency_window, amplitude_window):
"""窓あり・なしFFT比較"""
fig, (ax1, ax2) = plt.subplots(2, 1, figsize=(14, 10))
ax1.plot(t, mixed_signal, '--', label='y(t)')
ax1.plot(t, mixed_signal_window, label='y(t)h(t)')
ax1.grid(True, alpha=0.3)
ax1.legend()
ax2.
次回予告
一旦、「Pythonで学習するFFT解析(高速フーリエ変換解析)」シリーズは終わりの予定です。他になにか思いついたら記事を書くかもしれません。





コメント