【第4回】
ノイズの影響
本記事では、FFTにおけるノイズの影響について説明します。この記事を読むことで、ノイズ(ホワイトノイズ・ピンクノイズ・インパルスノイズ)がFFTの結果に与える影響がわかるようになります。本記事を読めば、3種のノイズのFFT結果への影響をテストデータを使って視覚的に理解することができます。
現実世界において、FFT解析とノイズは切っても切り離せない関係にあります。というのも何かデータを取得するとき、そこには必ずノイズが含まれるためです。例えば、加速度ピックアップで加速度を取得しようとしても、電気的なノイズや周辺環境の振動の影響などで、本来取得したいデータとは別のノイズ成分が含まれてしまうのです。このノイズとうまく付き合っていくことが、FFTを使いこなすうえで重要です。
本記事を読む前に、Pythonで学習するFFT解析シリーズの➀~➂までを事前に読むことを強くお勧めします。以前の記事はこちら。
ノイズの種類
今回は➀ホワイトノイズ➁ピンクノイズ➂インパルスノイズの3種のノイズについて説明します。まずは3つのノイズのFFTにおける特徴を説明します。テストデータのw(t)における部分が単独でどのような挙動を示すのかを理解してください。ホワイトノイズ・ピンクノイズ・インパルスノイズ、この3つはFFTにかけるとそれぞれ違った挙動をするのでそれを実データをみながら確認していきます。
ホワイトノイズ
ホワイトノイズの連蔵時間領域の定義は以下となります。この式が意味するところは、まず1行目に関してはホワイトノイズはとある時間区間で平均値をとるとその期待値としては0になるということを示しています。無限に長い時間のノイズを取得して平均したら、その平均値は0になるということです。2行目が意味するところは、とある時間で取得したノイズを2乗して、それを無限に長い時間で実施したものを足し合わせて平均したらsigma^2になり、とある時間のノイズとそれと少しでも違う時間のノイズで掛け合わせたものを無限時間足して平均したら0になる、という意味です。これを自己相関がsigma^2であり、相互相関が0である、とか数学的に言ったりします。
\[E[w(t)] = 0 \\
E[w(t)\,w(t-\tau)] =
\begin{cases}
\sigma^2, & \tau = 0 \\
0, & \tau \neq 0
\end{cases}
\]
そしてこのホワイトノイズw(t)をフーリエ変換すると、ホワイトノイズのパワースペクトルW(omega)は以下の式で表れます」。
\[|W(f)|^2 = \sigma^2\]これが意味するところは、ホワイトノイズは周波数領域においては、周波数に関わらず一定の値を取るということです。
ただし、注意点として、この式はホワイトノイズが無限に長い時間を取得した場合を前提とした式であり、実世界の有限の時間で取得したホワイトノイズでは、厳密には成り立ちません。どういうことかというと、有限時間で取得したホワイトノイズの平均値は厳密に0になるわけではないし、そのFFTの値も正確に定数になるわけではない、ということです。
ここでホワイトノイズを実際に生成し、そのFFTの結果を見てみましょう。
以下の3つの図を見てください。上が時間領域データ、下が周波数領域データ(FFTの結果)です。1つ目、2つ目、3つ目のプロットはホワイトノイズの標準偏差σは2.0で共通ですが、FFTの元となる時間領域データを2.0秒、10秒、50秒間サンプリングしています。サンプリング周波数は500Hzで固定なので、データ点数が1000点、5000点、25000点となっています。それぞれのプロットの時間領域データの方は、信号を見やすくするため最初の0.5秒間だけ表示していますが、実際は、2.0秒、10秒、50秒間分のデータがあります。
見てわかる通り、サンプリング時間が長くなればなるほど、FFTの結果としての振幅がある一定の数値に収束していっていることがわかります。逆にサンプリング時間が短いものにはFFTの結果にもランダム性が色濃く残ってしまっています。時間領域の信号は見ての通り特に振幅や周波数は変わっていないのに、サンプリング時間を長くとるだけでこのような変化が現れます。もう少し現実世界に深くつっこむと、とある測定をしている時に、ホワイトノイズ成分を落とすためにはサンプリング時間を長く取ればよい、ということになります。
ちなみに時間領域のサンプリング時間が長くなると、FFTの結果の周波数分解能が上がるのは前回説明しました。もしこれがピンとこない人は前々回の記事を読んで復習することをお勧めします。(前々回の記事はこちら)
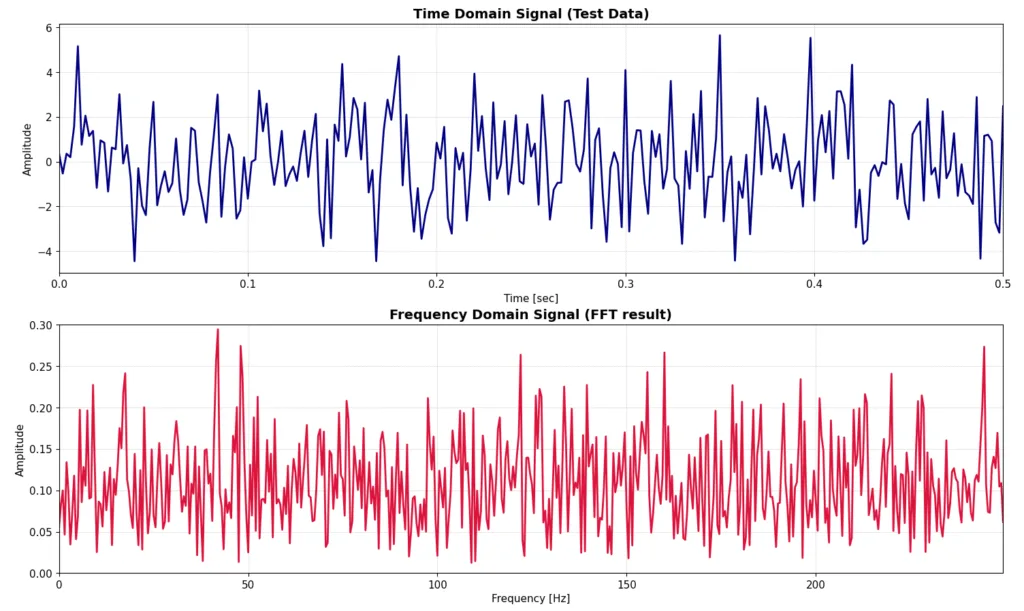
➀ 標準偏差 σ = 2.0, サンプリング時間 t = 2.0 [sec], サンプリング周波数 fs = 500 [Hz]
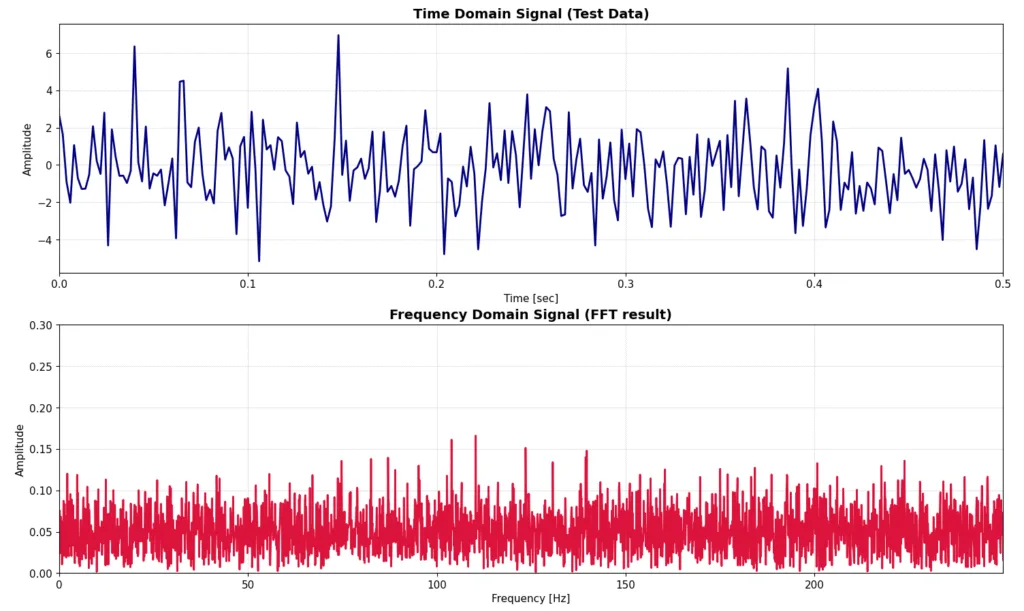
➁ 標準偏差 σ = 2.0, サンプリング時間 t = 10.0 [sec], サンプリング周波数 fs = 500 [Hz]
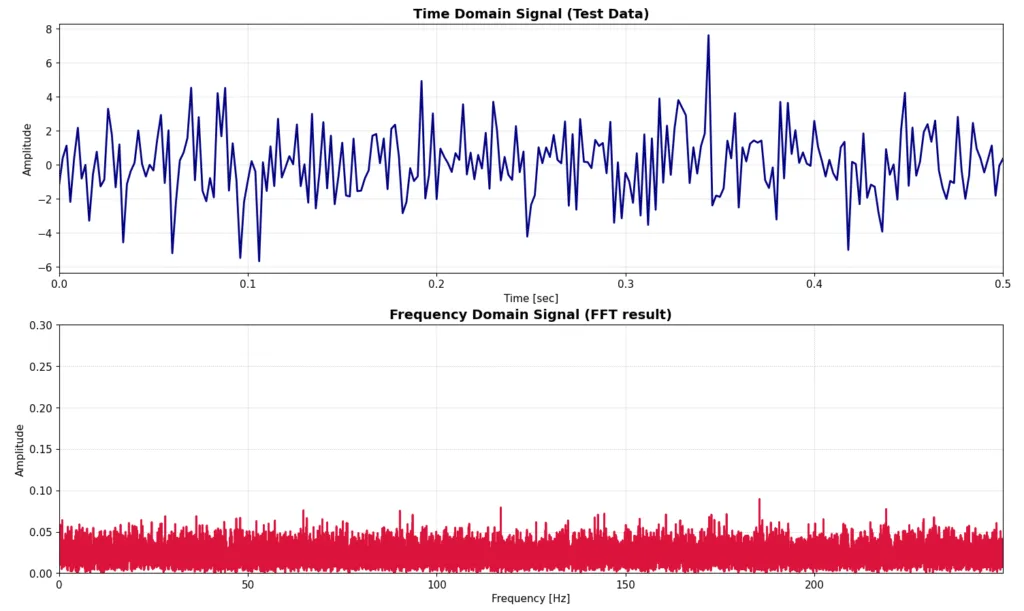
➂ 標準偏差 σ = 2.0, サンプリング時間 t = 50.0 [sec], サンプリング周波数 fs = 500 [Hz]
ピンクノイズ
ピンクノイズとは、1/fノイズとも呼ばれ、周波数fに応じて1/fにパワーが減衰していくという特徴を持ちます。式で書くと以下のように表すことができます。
\[S_w(f) = \frac{K}{f}\]ここで
\[\begin{array}{ll}
S_w(f) & :パワースペクトル密度\\
K &:定数\\
\end{array}
\]
パワースペクトル密度Sxとは各周波数にどれだけのパワー(エネルギー)を持つかを示しているものです。ここはあまり深く突っ込むとややこしいのでピンクノイズw[n]のDFT(FFT)の結果|W[k]|との関係だけ示します。パワースペクトル密度は|W[k]|を使って以下の式で表されます。
\[S_w(f_k) = \frac{1}{N f_s}\, |W[k]|^2\]ここでfsはサンプリング周波数、Nはデータ点数です。つまりパワースペクトル密度Sxはパワースペクトル|X[k]|^2をサンプリング時間で割ってスケーリングしたものになるということです。上記の式をつなげると、ピンクノイズのFFTの結果は以下の式のように表すことができます。
\[|W[k]| \propto \frac{1}{\sqrt{f_k}}\]実際にピンクノイズを生成して、FFTした結果が以下になります。FFTの結果をみてわかる通り、低周波の振幅が大きく、高周波の振幅が小さいということがわかります。理屈上は1/sqrt(f)に従うのですが、有限時間内のデータ点数であれば図のようにギザギザします。
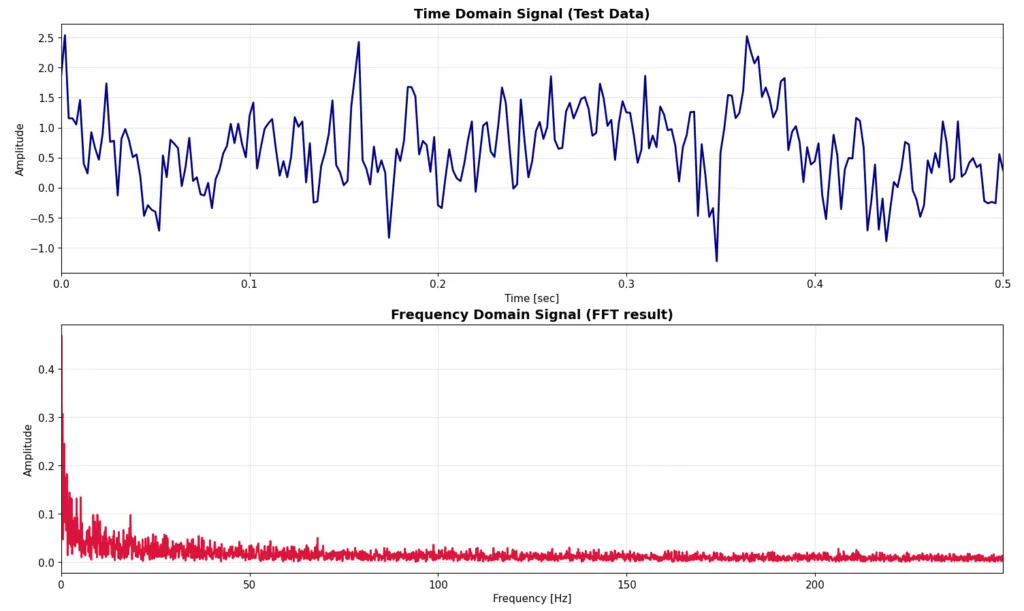
ちなみにピンクノイズは、自然界に非常に普遍的で「もっとも自然なノイズ」とも言われており、人間が心地よいと感じるノイズです。1/f揺らぎともよく言われていますね。以下のような現象もピンクノイズに従うといわれています。
- 電子デバイスのゆらぎ(フリッカーノイズ)
- 心拍間隔の揺らぎ
- 気温・河川流量のゆらぎ
- 音楽・自然音の統計的特徴
- 焚火やろうそくなどの炎の揺らぎ
インパルスノイズ
最後にインパルスノイズを説明します。インパルスノイズは、連続時間では以下の式で最後にインパルスノイズを説明します。インパルスノイズw(t)は、連続時間では以下の式で表されます。
\[w(t) = \sum_{i} A \, \delta(t – t_i)\]そしてこれを離散化したもの、つまりインパルスノイズの離散式w[n]は以下の式で表されます。
\[w[n] = \sum_{i} A \, \delta[n – n_i]\]ここで
\[\begin{array}{ll}
A & :インパルスノイズの大きさ\\
n_i & :インパルスノイズが発生するサンプル番号 \\
\delta[n-n_i] & :クロネッカーのデルタ \\
\end{array}
\]
ただし、δはクロネッカーのデルタと呼ばれ、以下の式で表されます。
\[\delta[n – n_i] =
\begin{cases}
1, & n = n_i \\
0, & n \neq n_i
\end{cases}
\]
このインパルスノイズw[n]をFFTにかける、つまり以下のDFTの式に当てはめると以下の式になることがわかります。
\[\begin{aligned}
W[k] &= \sum_{n=0}^{N-1} w[n]\cdot \exp\left(-j\frac{2\pi kn}{N}\right) \\
&= A\cdot \exp\left(-j\frac{2\pi kn_i}{N}\right) \\
\end{aligned}
\]
exp(-j※)は単位円上の回転を表すので大きさは1になりますので、結局インパルスノイズw[n]をFFTした結果の振幅スペクトル|W[k]|は以下の式で表されます。
\[|W[k]| = A\]かなりシンプルになりましたね。この式からわかるように、インパルスノイズは時間領域では瞬間的な無限に大きな信号ですが、周波数領域に変換すると、各周波数に均一に分配されます。逆に言うとあらゆる周波数を均一の振幅で足し合わせるとインパルスノイズになるということです。(細かく言うとあらゆる周波数を位相をそろえて足し合わせる必要がありますが)。
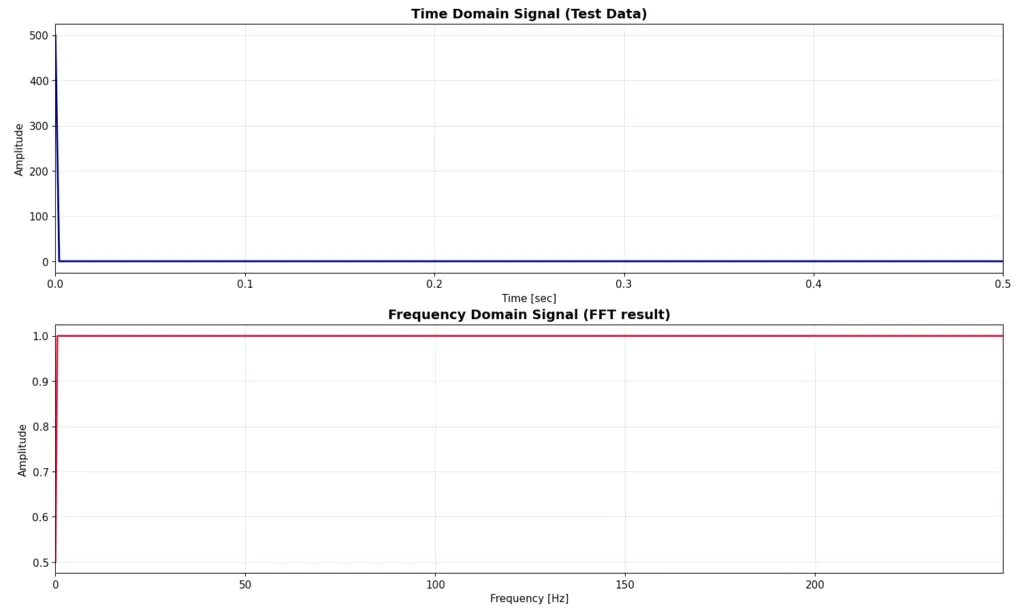
早速インパルスノイズのFFTの実例を見てみましょう。以下の図に時間領域でのインパルスノイズと、それをFFTにかけた結果をプロットしています。インパルスノイズの大きさはw[0] = fsとしました(こうすることで周波数領域での振幅は1になります)。
まとめ
3種類のノイズを説明しました。改めてそれらの特徴をまとめておきます。
- ホワイトノイズ:
- 時間領域:ランダムで正規分布に従う信号
- 周波数領域:統計的には各周波数で均一な値になる。
- ピンクノイズ:
- 時間領域:自然界に多いノイズ。低周波が強く、高周波が弱い。
- 周波数領域:パワースペクトルが1/fに比例。(振幅スペクトルが1/sqrt(f)に比例)
- インパルスノイズ:
- 時間領域:無限小の時間に瞬間的に無限大の大きさの信号
- 周波数領域:各周波数で一定の値
テストデータのFFT解析結果
では最後にこれまでと同様に、テストデータを使って視覚的に理解していきましょう。今回のテストデータは以下の式で表されます。取り扱うテストデータとしては、この式で表される連続信号を500Hzのサンプリング周波数で2秒間取得したものになります。w(t)部分は先ほど説明した3つのノイズとなります。
\[y(t) = a_1 \sin\omega_1 t + a_2 \sin\omega_2 t + w(t)\]ここで
\[\begin{array}{ll}
a_1 = 3 & :周波数\omega_1の振幅 [\;\;] \\
\omega_1 = 2\pi \times 10 & :10\rm{Hz}の角周波数 \rm{ [rad/s] } \\
a_2 = 1.5 & :周波数\omega_2の振幅 [\;\;] \\
\omega_2 = 2\pi \times 30 & :30\rm{Hz}の角周波数 \rm{ [rad/s] } \\
w(t):ノイズ成分
\end{array}
\]
ホワイトノイズ
w(t)がホワイトノイズだった場合のテストデータのFFTがどのようになるか説明します。まず、以下に時間領域信号をプロットしました。左上、右上がそれぞれメインとなるsin波の信号、左下がw(t)ホワイトノイズ、右下が最終足し合わせたy(t)の信号です。ただし、横軸は見やすくするために最初の0.5sだけ表示しています。
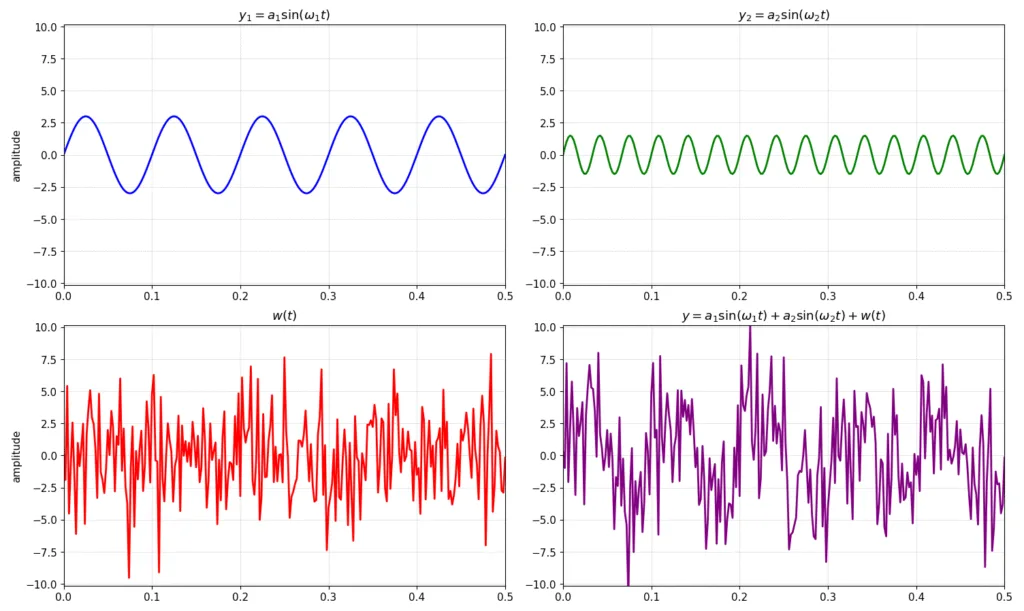
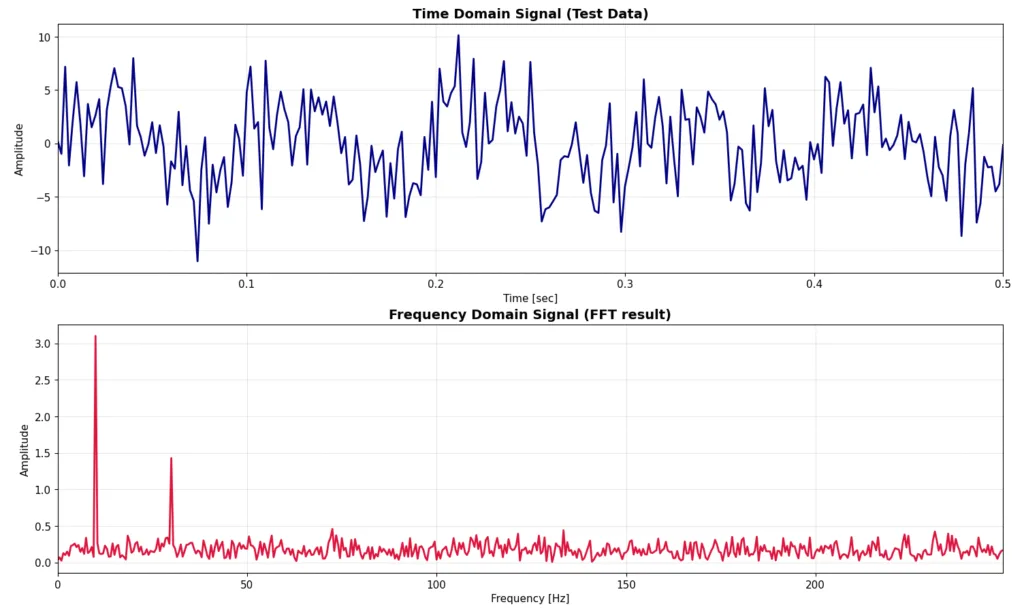
このy(t)をFFTした結果を以下に示します。上のプロットがy(t)の時間領域信号、でしたがFFTの結果です。
見てわかる通り、10Hz、30Hzのピークの他に、各周波数におおよそ均一なノイズ成分が乗ってきていることがわかります。このノイズ成分を小さくするためには、先ほども説明した通り、FFTにかける元の信号を長くすることで、ノイズ成分を小さくし、より正確な周波数解析ができます。
ピンクノイズ
次にw(t)がピンクノイズだった場合を見てみましょう。こちらもまずは以下に時間領域のプロットを示しました。
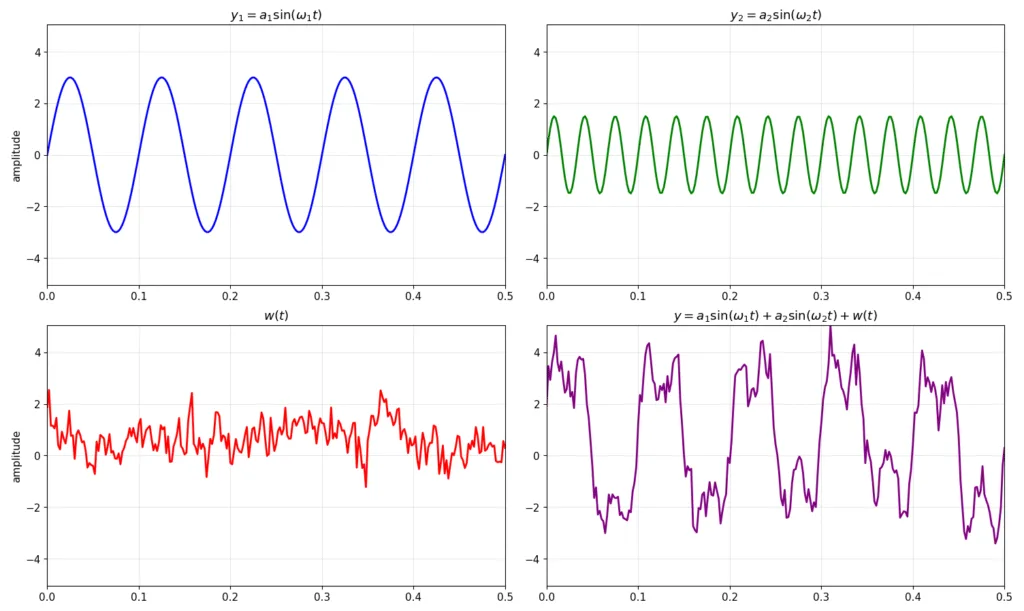
この時間領域信号をFFTした結果を以下に示します。見てわかる通り、10Hz、30Hzに主信号のピークがたっていますが小さくノイズ成分が乗っています。そして、そのノイズ成分は低周波に強く表れ、高周波では小さくなっていることがわかります。これがピンクノイズの特徴です。
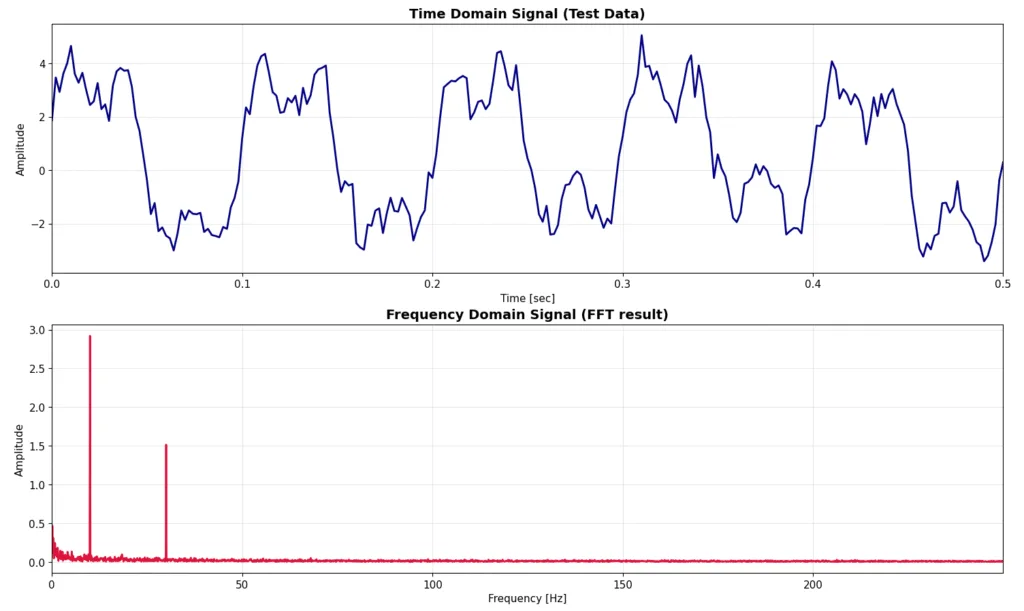
インパルスノイズ
最後にノイズw(t)がインパルスノイズだった場合を見ましょう。w[0]が500だった場合の時間領域信号は以下のようになります。
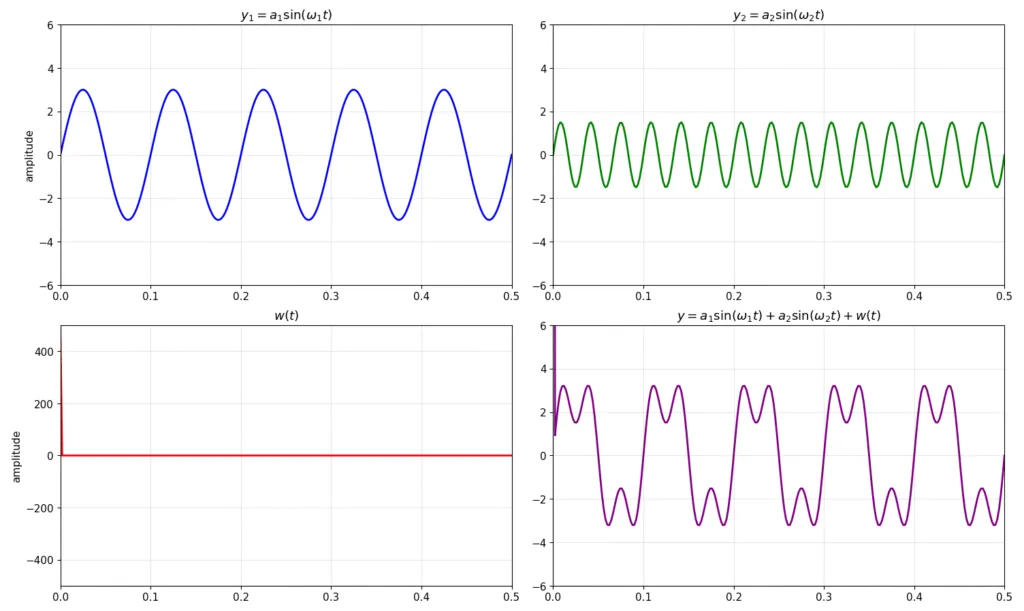
これをFFTかけた結果が以下になります。瞬間的に500の振幅のノイズが入るため、時間領域のプロットの方は縮尺的に主信号がほぼ見えなくなっています。そして周波数領域の信号を見ると、各周波数に振幅1の均一のオフセットがかかったような結果となっています。インパルスノイズは周波数解析する際に、オフセットがかかるだけなので影響度としては小さいですね。
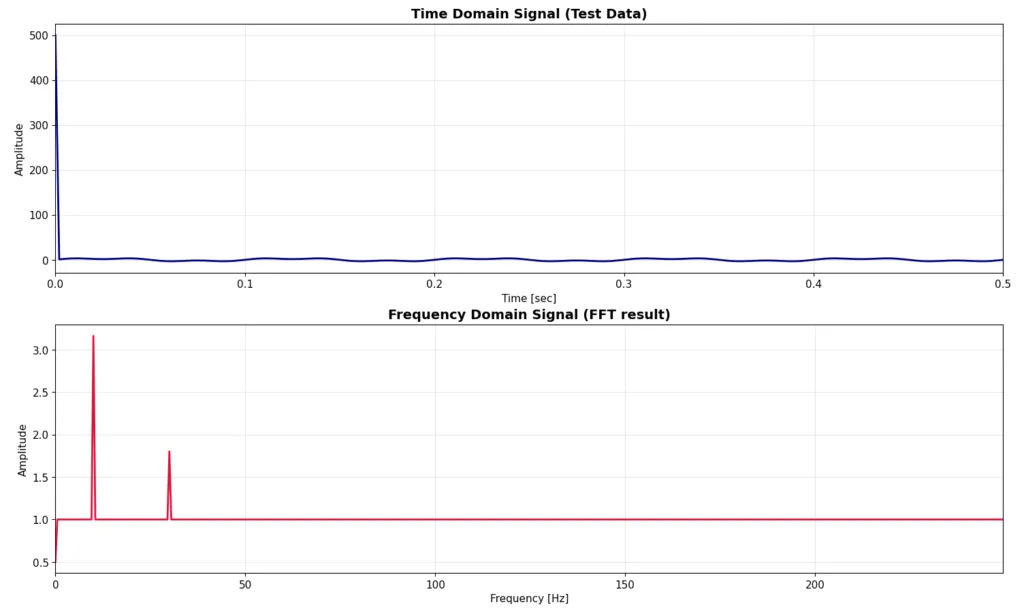
Python実装コード
では最後に今回のFFT解析をどのようなpythonコードで実行したか見てみましょう。いつも通り、メインプログラムと、関数ファイルに分かれています。
メインプログラム(main.py)
24,27,30行目に3つのノイズを生み出すコードを用意しました。適切にコメントアウトすることで、どのノイズにするか選択ができます。
import numpy as np
import FFT_lib as fft
# サンプリング設定
sampling_rate = 500 # 500Hz
duration = 2.0 # 2秒間
N = int(sampling_rate * duration) # 総サンプル数
# 時間軸を作成
t = np.linspace(0, duration, N, endpoint=False)
# サンプルデータの周波数と振幅を設定
freq1, freq2 = 10, 30 # Hz
amp1, amp2 = 3.0, 1.5 # 振幅
#ホワイトノイズの標準偏差を定義(ホワイトノイズ、ピンクノイズに使用)
noise_std = 5.0
# 2つの周波数が混合した信号を生成
signal1, signal2, mixed_signal = fft.generate_testData(t, freq1, freq2, amp1, amp2)
"""------以下、ノイズは3つのうち1つを選択すること------"""
#混合信号にホワイトノイズを追加(必要に応じてコメントアウト)
noise, mixed_signal_withNoise = fft.add_whiteNoise(mixed_signal, noise_std)
#混合信号にピンクノイズを追加(必要に応じてコメントアウト)
#noise, mixed_signal_withNoise = fft.add_pinkNoise(sampling_rate, mixed_signal, noise_std)
#混合信号にインパルスノイズを追加(必要に応じてコメントアウト)
#noise, mixed_signal_withNoise = fft.add_impulseNoise(sampling_rate, mixed_signal)
"""-----------------------------------------------"""
print(f"テストデータが作成されました:y(t) = {amp1}*sin(2π{freq1}t) + {amp2}*sin(2π{freq2}t) + w(t)")
# 生成した信号をプロット
t_short = 0.5 # 最初の0.5秒だけ表示
fft.plot_testData_withNoise(t, 0.5, signal1, signal2, noise, mixed_signal_withNoise)
print("時間領域での信号をプロットしました。")
#ノイズ成分のみのfFT解析を実行
frequency_noise, amplitude_noise, fft_result_noise = fft.execute_fft(noise, sampling_rate)
#ノイズ成分のみのFFT解析の結果をプロット
fft.plot_fftResult(t, t_short, noise, frequency_noise, amplitude_noise)
print("ノイズ成分のみのFFT解析結果をプロットしました。")
# テストデータ全体のFFT解析を実行
frequency, amplitude, fft_result = fft.execute_fft(mixed_signal_withNoise, sampling_rate)
print("FFT解析を実行しました。")
print(f"周波数分解能: {frequency[1] - frequency[0]:.2f} Hz")
print(f"最大周波数: {frequency[-1]:.0f} Hz (ナイキスト周波数)")
# テストデータ全体のFFT解析の結果をプロット
fft.plot_fftResult(t, t_short, mixed_signal_withNoise, frequency, amplitude)
print("FFT解析結果をプロットしました。")
関数ファイル(FFT_lib.py)
関数ファイルで特に説明が必要なところとしては、42行目以降のピンクノイズの作成方法のところぐらいかと思います。
ピンクノイズは振幅ペクトルが周波数の平方根に反比例するという特徴を生かして以下のように作成しています。
➀ホワイトノイズを作成
➁ホワイトノイズをFFTにかける
➂振幅スペクトルに1/sqrt(f)をかける
➃その結果得られたものを逆フーリエ変換にかける
import numpy as np
import matplotlib.pyplot as plt
from scipy.fft import fft, fftfreq, rfft, rfftfreq, irfft
# グラフを美しくする設定
plt.rcParams['figure.figsize'] = (12, 8)
plt.rcParams['font.size'] = 11
# 2つの周波数が混合した信号を生成
def generate_testData(t,freq1,freq2,amp1,amp2):
"""3つの周波数が混合した信号を生成
Takes :
t: 時間軸 [sec]
freq1, freq2: 周波数1, 2 [Hz]
amp1, amp2: 振幅1, 2 [ ]
Returns:
signal1, signal2: 個別の正弦波信号 [ ]
mixed_signal: 3つの信号を混合したもの [ ]
"""
#各周波数成分の信号
signal1 = amp1 * np.sin(2 * np.pi * freq1 * t)
signal2 = amp2 * np.sin(2 * np.pi * freq2 * t)
# 2つの信号を混合
mixed_signal = signal1 + signal2
return signal1, signal2, mixed_signal
def add_whiteNoise(original_singal, noise_std):
"""元の信号にホワイトノイズを追加
Takes : original_singal: 元の信号 [ ]
noise_std: ホワイトノイズの標準偏差 [ ]
Returns: white_noise: 生成したホワイトノイズ [ ]
noisy_signal: ホワイトノイズを追加した信号 [ ]
"""
#ホワイトノイズを生成
white_noise = np.random.normal(0, noise_std, size=original_singal.shape)
#ホワイトノイズを追加
noisy_signal = original_singal + white_noise
return white_noise, noisy_signal
def add_pinkNoise(sampling_rate,original_singal, noise_std):
"""元の信号にピンクノイズを追加
Takes : sampling_rate: サンプリング周波数 [Hz]
original_singal: 元の信号 [ ]
noise_std: ピンクノイズの標準偏差 [ ]
Returns: pink_noise: 生成したピンクノイズ [ ]
noisy_signal: ピンクノイズを追加した信号 [ ]
"""
N = len(original_singal)
#ホワイトノイズを生成
white_noise = np.random.normal(0, noise_std,N)
# FFT
W = rfft(white_noise)
# 周波数軸を作成
freqs = rfftfreq(N, 1/sampling_rate)
# 1/f のスペクトルにスケーリング(0Hzを除外)
W[1:] /= np.sqrt(freqs[1:])
# 逆FFTで時系列に戻す
pink_noise = irfft(W)
# ピンクノイズを追加
noisy_signal = original_singal + pink_noise
return pink_noise, noisy_signal
def add_impulseNoise(sampling_rate, original_singal):
"""元の信号にインパルスノイズを追加
Takes : sampling_rate: サンプリング周波数 [Hz]
original_singal: 元の信号 [ ]
Returns: impulse_noise: 生成したインパルスノイズ [ ]
noisy_signal: インパルスノイズを追加した信号 [ ]
"""
N = len(original_singal)
# インパルスノイズを生成
impulse_noise = np.zeros(N)
impulse_noise[0] = sampling_rate
# インパルスノイズを追加
noisy_signal = original_singal + impulse_noise
return impulse_noise, noisy_signal
def plot_testData_withNoise(t, t_short, signal1, signal2, white_noise, mixed_signal):
"""時間域での信号をプロット
Takes : t: 時間軸
t_short: 最初の何秒間を表示するか
signal1, signal2, signal3: 個別の正弦波信号
mixed: 3つの信号を混合したもの
Returns: None
"""
fig, axes = plt.subplots(2, 2, figsize=(15, 10))
mask = t <= t_short
t_short_list = t[mask]
# 縦軸範囲を全プロットで統一
y_max_abs = max(np.abs(signal1[mask].max()), np.abs(signal2[mask].max()), np.abs(mixed_signal[mask].max()))
# 個別信号
axes[0, 0].plot(t_short_list, signal1[mask], 'b-', linewidth=2, label='10Hz')
axes[0, 0].set_title(r'$y_1 = a_1 \sin(\omega_1 t)$', fontweight='bold')
axes[0, 0].grid(True, alpha=0.3)
axes[0, 0].set_ylabel('amplitude')
axes[0, 0].set_xlim(0, t_short)
axes[0, 0].set_ylim(-y_max_abs, y_max_abs)
axes[0, 1].plot(t_short_list, signal2[mask], 'g-', linewidth=2, label='30Hz')
axes[0, 1].set_title(r'$y_2 = a_2 \sin(\omega_2 t)$', fontweight='bold')
axes[0, 1].grid(True, alpha=0.3)
axes[0, 1].set_xlim(0, t_short)
axes[0, 1].set_ylim(-y_max_abs, y_max_abs)
#ノイズ成分
axes[1, 0].plot(t_short_list, white_noise[mask], 'r-', linewidth=2, label='60Hz')
axes[1, 0].set_title(r'$w(t)$', fontweight='bold')
axes[1, 0].grid(True, alpha=0.3)
axes[1, 0].set_ylabel('amplitude')
axes[1, 0].set_xlim(0, t_short)
axes[1, 0].set_ylim(-y_max_abs, y_max_abs)
# 混合信号
axes[1, 1].plot(t_short_list, mixed_signal[mask], 'purple', linewidth=2)
axes[1, 1].set_title(r'$y = a_1 \sin(\omega_1 t) + a_2 \sin(\omega_2 t) + w(t)$', fontweight='bold')
axes[1, 1].grid(True, alpha=0.3)
axes[1, 1].set_xlim(0, t_short)
axes[1, 1].set_ylim(-y_max_abs, y_max_abs)
plt.tight_layout()
plt.show()
def execute_fft(mixed_signal, sampling_rate):
"""信号にFFTを適用して周波数解析
Takes : signal: 入力信号 [ ]
sampling_rate: サンプリング周波数 [Hz]
Returns: frequencies_positive: 正の周波数成分 [Hz]
amplitude_single_sided: 片側振幅スペクトラム [ ]
fft_result: FFTの複素数結果 [ ]
"""
N = len(mixed_signal)
# FFT実行
fft_result = fft(mixed_signal)
# 周波数軸を作成
frequencies = fftfreq(N, 1 / sampling_rate)
# 振幅スペクトラムを計算(複素数の絶対値)
amplitude_spectrum = np.abs(fft_result)
# 正の周波数のみ取得(実信号の場合、負の周波数は冗長)
positive_freq_mask = frequencies >= 0
frequencies_positive = frequencies[positive_freq_mask]
amplitude_positive = amplitude_spectrum[positive_freq_mask]
# 片側振幅スペクトラムに変換(DC成分以外は2倍)
amplitude_single_sided = amplitude_positive * 2 / N
amplitude_single_sided[0] = amplitude_positive[0] / N
return frequencies_positive, amplitude_single_sided, fft_result
def plot_fftResult(t, t_short, mixed_signal, frequency, amplitude):
"""FFT結果を美しく可視化(片側振幅スペクトラム)
Takes : t: 時間軸
t_short: 最初の何秒間を表示するか
mixed_signal: 3つの信号を混合したもの
frequency: 周波数軸 [Hz]
amplitude: 片側振幅スペクトラム [ ]
Returns: None
"""
fig, (ax1, ax2) = plt.subplots(2, 1, figsize=(14, 10))
# 上段:時間領域
time_mask = t <= t_short
ax1.plot(t[time_mask], mixed_signal[time_mask], 'navy', linewidth=2)
ax1.set_title('Time Domain Signal (Test Data)', fontsize=14, fontweight='bold')
ax1.set_xlabel('Time [sec]')
ax1.set_ylabel('Amplitude')
ax1.set_xlim(0, t_short)
ax1.grid(True, alpha=0.3)
# 下段:周波数領域
ax2.plot(frequency, amplitude, 'crimson', linewidth=2)
ax2.set_title('Frequency Domain Signal (FFT result)', fontsize=14, fontweight='bold')
ax2.set_xlabel('Frequency [Hz]')
ax2.set_ylabel('Amplitude')
ax2.set_xlim(0, frequency[-1])
ax2.grid(True, alpha=0.3)
plt.tight_layout()
plt.show()
Tips
scipy.fftには、scipy.fft.fft()と、scipy.fft.rfft()の2種類のfftのメソッドが存在します。これらの違いがどのようなところにあるのか、公式を引用しながら説明します。
まずはfft()の方を確認してみます。入力信号を入れるxの部分に、can be complexという表記があります。つまりfft()の方は入力信号が複素数の場合も想定したmethodになっています。
fft(x, n=None, axis=-1, norm=None, overwrite_x=False, workers=None, *, plan=None)This function computes the 1-D n-point discrete Fourier Transform (DFT) with the efficient Fast Fourier Transform (FFT) algorithm.
Parameters:
x : x array_like
Input array, can be complex.
他は割愛
Returns:
out:complex ndarray
The truncated or zero-padded input, transformed along the axis indicated by axis, or the last one if axis is not specified.
一方でrfft()の方を見てみましょう。説明に real-valued arrayを書いてあるように、入力は実数であることを前提にしたmethodになっています。おそらくこのrfft()のrはrealのrだと思われます。
rfft(x, n=None, axis=-1, norm=None, overwrite_x=False, workers=None, *, plan=None)This function computes the 1-D n-point discrete Fourier Transform (DFT) of a real-valued array by means of an efficient algorithm called the Fast Fourier Transform (FFT).
Parameters:
x : x array_like
Input array
他は割愛
Returns:
out:complex ndarray
The truncated or zero-padded input, transformed along the axis indicated by axis, or the last one if axis is not specified.
If n is even, the length of the transformed axis is
(n/2)+1. If n is odd, the length is(n+1)/2.
ではrfft()とfft()を使用するのにどのような違いが出るのでしょうか?
実世界において周波数解析を実施するための時間領域データが複素数であることはほとんどありません。つまり入力はほとんどのケースで実数になります。この実数の入力xをrfft()、fft()にかけて得られる周波数解析の情報としては実は同じになります。ただし、rfft()の方が計算量が少なく、軽い処理となります。なぜ軽くなるかというと、入力がすべて実数だった場合、FFTで得られた|X[k]|はナイキスト周波数を境目に折り返しが発生し、正の周波数と負の周波数で対称な結果が得られるため、負の周波数は実質情報が不要となります。rfft()の方はその負の周波数部分の計算をしないため、計算が軽くなるのです。そのため、fft()の戻り値が次元nの大きさを持つのに対し、rfft()の戻り値は次元(n/2)+1 or (n+1)/2の大きさしか持たないのです(nが奇数か偶数かによって異なる)。
実運用ではほぼrfft()で事足りるため、積極的にrfft()を使っていきましょう。
When the DFT is computed for purely real input, the output is Hermitian-symmetric, i.e., the negative frequency terms are just the complex conjugates of the corresponding positive-frequency terms, and the negative-frequency terms are therefore redundant. This function does not compute the negative frequency terms, and the length of the transformed axis of the output is therefore
n//2 + 1.
実際に今回の関数ファイルの54,56行目でもrfft()、rfftfreq()を使用しています。rfftfreq()は、正の周波数だけを作る関数です。
次回予告
次回はFFTをかけた際のスペクトル漏れ(リーケッジ誤差)と窓関数について説明しようと思います。





コメント