【第3回】
位相遅れとDC成分編
本記事では、FFTにおける位相遅れとDC成分について説明します。本記事を読むことで、実データをFFT解析した際に位相遅れとDC成分がどのように結果に表れるかを視覚的に理解できます。また、実例をpythonで実際に実装しながらこれを説明しますので、pythonでのデータの取り扱い方法も理解できます。
この記事はシリーズとなっているので、FFTの概要や基本的なpython実装に関しては、以前の記事に軽く目を通すことを強くお勧めします。以前の記事ははこちら(Pythonで学習するFFT解析➀、Pythonで学習するFFT解析➁)。
位相遅れとDC成分を含んだテストデータ
テストデータの式
テストデータは以下の式で表されるものを、500Hzで2秒間サンプリングした時間領域離散信号とします。
\[y(t) = a_1 \cos(\omega_1 t+\theta_1) + a_2 \cos(\omega_2 t+\theta_2) + a_3 \cos(\omega_3 t+\theta_3)+C\]ここで
\[\begin{array}{ll}
a_1 = 3 & :周波数\omega_1の振幅 [\;\;] \\
\omega_1 = 2\pi \times 10 & :10\rm{Hz}の角周波数 \rm{ [rad/s] } \\
\theta_1 = 0 &: 周波数\omega_1の位相遅れ \rm{[rad]}\\
a_2 = 1.5 & :周波数\omega_2の振幅 [\;\;] \\
\omega_2 = 2\pi \times 30 & :30\rm{Hz}の角周波数 \rm{ [rad/s] } \\
\theta_2 = \frac{\pi}{4} &: 周波数\omega_2の位相遅れ \rm{[rad]}\\
a_3 = 0.8 & :周波数\omega_3の振幅 [\;\;] \\
\omega_3 = 2\pi \times 60 & :60\rm{Hz}の角周波数 \rm{ [rad/s] } \\
\theta_3 = -\frac{\pi}{2} &: 周波数\omega_3の位相遅れ \rm{[rad]}\\
C = 1.0 & : \rm{DC成分(周波数0の成分)}\\
\end{array}
\]
前回、前々回の式と比較して、①各周波数に位相遅れΘ1,Θ2,Θ3が付加されたこと、➁sinではなくcosになっていること、➂定数項(DC成分)が付加されていること、の3点が差分としてあります。➀➂に関しては、今回の「位相遅れ」「DC成分」を説明するために追加したもので、➁に関しては説明の都合で変えています。後でなぜcosに変えたかはわかります。サンプリング周波数も500 Hzに変わっていますが、これもグラフを見やすくするための都合ですので特に意味はありません。(入力周波数はすべてナイキスト周波数以下なので解析への影響もありません。)
※ちなみに定数項をDC成分とは、信号の値が時間によって変化しない「直流」の成分を表しており、Direct Currentの略称です。「交流」の意味のAC成分(Alternative Current)と対義語として使われ主に、電気分野でよく使われる呼び方です。意味としては定数項(時間変化しない)と同じです。
テストデータの可視化
上記の式で表される信号をプロットすると、以下のようになります。
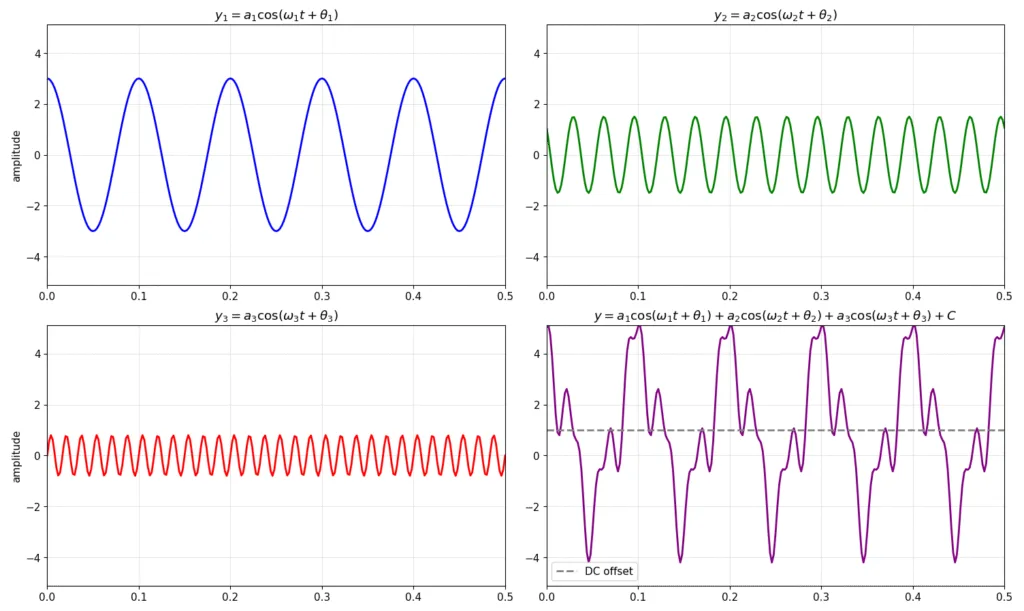
青・赤・緑はそれぞれのa*cos(wt+Θ)の部分だけ表記したもので、右下の紫のプロットが、それら3つの周波数成分とDC成分を足し合わせたy(t)を表しています。グレー点線がDC成分であり、DC成分の1だけ0からオフセットしたところを中心に振動しているような信号になっていることがわかります。
青のプロットは、位相遅れΘ1 = 0なので、遅れのないcosカーブになっています。緑のプロットは位相遅れΘ2 = pi/4なので、pi/4だけ位相が進んだプロットとなっています。赤のプロットは位相遅れΘ3=-pi/2なので、pi/2だけ位相が遅れたプロット(結果的にsinカーブ)になっています。
これで位相遅れと、DC成分を含んだテストデータの作成は完了です。
FFT解析の実行
おさらいですが、FFTの背景にある式はDFTです。そのDFTの一般式は離散入力信号x[n]に対し(今回の実例ではy[n])、以下の式で表されます(Pythonで学習するFFT解析➀参照)。
\[X[k] = \sum_{n=0}^{N-1} x[n] \cdot \exp\left(-j\frac{2\pi kn}{N}\right)\]上記式で得られるX[k]を周波数スペクトルや、複素スペクトルと呼びます。今回は複素スペクトルといった方が説明しやすいので複素スペクトルと呼ぶことにします。
今回の実例に当てはめるなら、上記式のx[n]の部分に、位相遅れとDC成分が入ったテストデータy(t)の離散信号y[n]が入ると考えてください。
FFT解析におけるDC成分
先ほどの複素スペクトルX[k]の絶対値を取ることで振幅が得られることは前回説明した通りです。ただし、注意しないといけないのがDC成分に関しては、他の周波数成分と異なり、2倍してはいけません。(Pythonで学習するFFT解析➁に詳細は記載)。このA0を計算すると、元の入力データに含まれるDC成分が値として得られるわけです。
\[\begin{array}{ll}
A_0 = \frac{1}{N}\left|X[0]\right|& :DC成分(k=0 の 0 \rm{Hz}部分)\\
A = \frac{2}{N} \left| X[k] \right|& :k\neq0(0 \rm{Hz}以外の部分)\\
\end{array}
\]
ちなみにDC成分は、周波数ゼロの成分なのでX[0]の値が対応しますが、このX[0]は常に実数になります。(複素数になりません)。というのも、DFTの式にk=0を代入してもらえると以下の式となり、入力信号が実数である限り、X[0]も常に実数となるのです。
\[X[0] = \sum_{n=0}^{N-1} x[n]\]FFT解析における位相遅れ
次に位相遅れですが、位相遅れは複素スペクトルX[k]に対して以下を計算することで、位相遅れの情報が得られます。
\[\theta[k] = \arg\!\left( X[k] \right)\]ただしΘは以下の範囲で得られます。
\[ -\pi \leq \theta[k] \leq \pi\]このargというのは、複素数X[k]に対して実部と虚部の割合からarctanを計算して角度を取得するようなものです。これによって、各周波数に対する位相遅れの情報が得られます。遅れの範囲が-piからpiなのは、sin波、cos波はそれ以上遅れたとしても結局-piからpiの範囲で遅れた信号と全く同等に見えるため意味をなさないので、-piからpiの間で定義しきることができるのです。
ちなみに先ほど説明したDC成分は、X[0]が実数であるため、arg(X[0])も常に0となり、周波数0の周波数遅れは発生しません。よく考えたらあり前で、時間領域でプロットしたら横一直線になるDC成分に遅れもへったくれもないのです。
位相遅れに関して、python実装上で1点注意すべきことは、振幅が0の周波数の位相遅れ情報は意味がないということ、です。振幅がゼロなので、もちろんX[k]の絶対値|X[k]|もゼロになり、arg(X[k])の計算もゼロで割り算するようなものになってしまいます。そしてプログラミング上、必ず丸め誤差や数値誤差が発生し、この小さな誤差にarg(X[k])の情報が大きく左右されることになってしまいます。ですので、振幅がほぼ0の周波数に関する位相情報は無視するべきで、今回の私の実装上もそのようにしています。(詳しくは後述の実装コードを確認してください。)
FFT解析結果の可視化
では上記の理屈を念頭に置いて、位相遅れとDC成分を含んだテストデータy(t)をFFT解析した結果を見てみましょう。
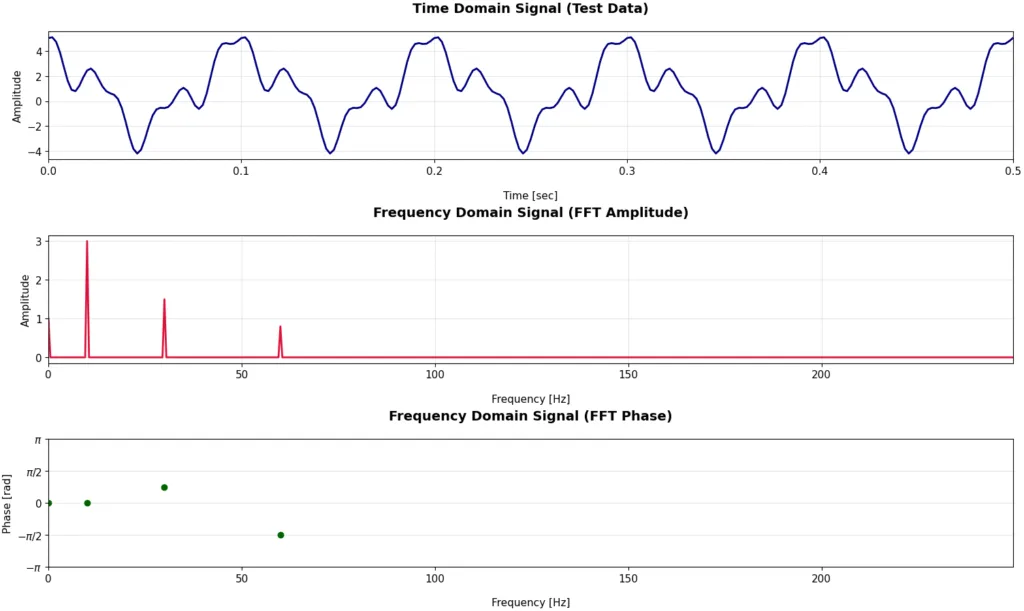
以下に示す図の一番上の青のプロットが時間領域の信号y(t)の最初の0.5秒分のプロットです。下の赤のプロットがFFT解析した結果の振幅を示したものです。DC成分は周波数0のところが対応しますが、しっかり振幅が1となってピークがたっていることがわかります。そして、一番下の緑のプロットが位相遅れ情報です。振幅が0の部分はマスクしているため、0, 10, 30, 60Hzの部分だけ位相遅れの情報をプロットしています。0, 10Hzは遅れ0 rad、30Hzは遅れ(進み)pi/4、60Hzは遅れ-pi/2となっており、見事にもとの入力信号の情報を復元できています。
ここで今回入力信号をsinではなくcosにした理由のタネを明かすと、FFT(DFT)は入力信号がcos波であることを前提に位相情報が出力されるためです。なので入力信号がsin波だった場合はpi/2だけずれた結果が位相情報として出てくることになります。今回は説明をわかりやすくするためにcosを使ったのです。
最後に
ここまで、FFT解析における位相遅れの解説をしましたが、正直とある1つのデータセットに対する位相遅れの情報は、現実世界ではあまり強い意味はありません。というのも、データ取得開始のタイミング次第で、位相が遅れているのか進んでいるのかは変わってしまうためです。強いて言うなら、とある周波数に対して、別の周波数の位相がどれだけ相対的に遅れているかを見る程度です。やはりどちらかというと振幅の情報の方が現実世界ではよく使います。
位相情報は、むしろシステム同定などをする際に使われることが多く、共振周波数を探す際に、「共振周波数前後で位相が逆転する」という特徴を用いて、共振周波数特定に使われることが多いです。
Python実装コードの紹介
メインプログラム(main.py)
今回のメインプログラムは以下の通りです。前回の実装から位相遅れ情報と、dc成分が追加された部分が差分としてあります。
import numpy as np
import FFT_lib as fft
# サンプリング設定
sampling_rate = 500 # 500Hz(1秒に500回測定)
duration = 2.0 # 2秒間
N = int(sampling_rate * duration) # 総サンプル数
# 時間軸を作成
t = np.linspace(0, duration, N, endpoint=False)
# サンプルデータの周波数と振幅を設定
freq1, freq2, freq3 = 10, 30, 60 # Hz
phase1, phase2, phase3 = 0, np.pi/4, -np.pi/2 # 位相
amp1, amp2, amp3 = 3.0, 1.5, 0.8 # 振幅
dc_offset = 1.0 # DCオフセット
# 3つの周波数が混合した信号を生成
signal1, signal2, signal3, mixed_signal = fft.generate_testData(
t, freq1, freq2, freq3, amp1, amp2, amp3, phase1, phase2, phase3, dc_offset)
print(f"テストデータが作成されました:y(t) = {amp1}*cos(2π{freq1}t+{phase1}) + {amp2}*cos(2π{freq2}t+{phase2}) + {amp3}*cos(2π{freq3}t+{phase3})+{dc_offset}")
# 生成した信号をプロット
t_short = 0.5 # 最初の0.5秒だけ表示
fft.plot_testData(t, 0.5, signal1, signal2, signal3, mixed_signal, dc_offset)
print("時間領域での信号をプロットしました。")
# FFT解析を実行
frequency, amplitude, phase, fft_result = fft.execute_fft(mixed_signal, sampling_rate)
print("FFT解析を実行しました。")
print(f"周波数分解能: {frequency[1] - frequency[0]:.2f} Hz")
print(f"最大周波数: {frequency[-1]:.0f} Hz (ナイキスト周波数)")
# FFT解析の結果をプロット
fft.plot_fftResult(t, t_short, mixed_signal, frequency, amplitude, phase)関数ファイル(FFT_lib.py)
今回の関数ファイルは以下です。位相遅れとDC成分が追加されたため、関数の引数が増えています。
また125,126行目には振幅が0の部分の位相遅れをマスキングしている部分の実装を示しています。
import numpy as np
import matplotlib.pyplot as plt
from scipy.fft import fft, fftfreq
# グラフを美しくする設定
plt.rcParams['figure.figsize'] = (12, 8)
plt.rcParams['font.size'] = 11
# 3つの周波数が混合した信号を生成
def generate_testData(t,freq1,freq2,freq3,amp1,amp2,amp3,phase1,phase2,phase3,dc_offset):
"""3つの周波数が混合した信号を生成
Takes :
t: 時間軸 [sec]
freq1, freq2, freq3: 周波数1, 2, 3 [Hz]
amp1, amp2, amp3: 振幅1, 2, 3 [ ]
phase1, phase2, phase3: 位相遅れ [rad]
dc_offset: DCオフセット [ ]
Returns:
signal1, signal2, signal3: 個別の正弦波信号 [ ]
mixed_signal: 3つの信号を混合したもの [ ]
"""
signal1 = amp1 * np.cos(2 * np.pi * freq1 * t + phase1)
signal2 = amp2 * np.cos(2 * np.pi * freq2 * t + phase2)
signal3 = amp3 * np.cos(2 * np.pi * freq3 * t + phase3)
# 3つの信号を混合し、DCオフセットを加算
mixed_signal = signal1 + signal2 + signal3 + dc_offset
return signal1, signal2, signal3, mixed_signal
def plot_testData(t, t_short, signal1, signal2, signal3, mixed_signal, dc_offset):
"""時間域での信号をプロット"""
fig, axes = plt.subplots(2, 2, figsize=(15, 10))
mask = t <= t_short
t_short_list = t[mask]
# 縦軸範囲を全プロットで統一
y_min = min(signal1[mask].min(), signal2[mask].min(), signal3[mask].min(), mixed_signal[mask].min())
y_max = max(signal1[mask].max(), signal2[mask].max(), signal3[mask].max(), mixed_signal[mask].max())
y_abs_max = max(np.abs(y_min), np.abs(y_max))
# 個別信号
axes[0, 0].plot(t_short_list, signal1[mask], 'b-', linewidth=2, label='10Hz')
axes[0, 0].set_title(r'$y_1 = a_1 \cos(\omega_1 t+\theta_1)$', fontweight='bold')
axes[0, 0].grid(True, alpha=0.3)
axes[0, 0].set_ylabel('amplitude')
axes[0, 0].set_xlim(0, t_short)
axes[0, 0].set_ylim(-y_abs_max, y_abs_max)
axes[0, 1].plot(t_short_list, signal2[mask], 'g-', linewidth=2, label='30Hz')
axes[0, 1].set_title(r'$y_2 = a_2 \cos(\omega_2 t+\theta_2)$', fontweight='bold')
axes[0, 1].grid(True, alpha=0.3)
axes[0, 1].set_xlim(0, t_short)
axes[0, 1].set_ylim(-y_abs_max, y_abs_max)
axes[1, 0].plot(t_short_list, signal3[mask], 'r-', linewidth=2, label='60Hz')
axes[1, 0].set_title(r'$y_3 = a_3 \cos(\omega_3 t+\theta_3)$', fontweight='bold')
axes[1, 0].grid(True, alpha=0.3)
axes[1, 0].set_ylabel('amplitude')
axes[1, 0].set_xlim(0, t_short)
axes[1, 0].set_ylim(-y_abs_max, y_abs_max)
# 混合信号+DCオフセットの直線
axes[1, 1].plot(t_short_list, mixed_signal[mask], 'purple', linewidth=2)
axes[1, 1].axhline(dc_offset, color='gray', linestyle='--', linewidth=2, label='DC offset')
axes[1, 1].set_title(r'$y = a_1 \cos(\omega_1 t+\theta_1) + a_2 \cos(\omega_2 t+\theta_2) + a_3 \cos(\omega_3 t+\theta_3) + C$', fontweight='bold')
axes[1, 1].grid(True, alpha=0.3)
axes[1, 1].set_xlim(0, t_short)
axes[1, 1].set_ylim(-y_abs_max, y_abs_max)
axes[1, 1].legend()
plt.tight_layout()
plt.show()
def execute_fft(mixed_signal, sampling_rate):
"""信号にFFTを適用して周波数解析"""
N = len(mixed_signal)
# FFT実行
fft_result = fft(mixed_signal)
# 周波数軸を作成
frequencies = fftfreq(N, 1 / sampling_rate)
# 振幅スペクトラムを計算(複素数の絶対値)
amplitude_spectrum = np.abs(fft_result)
# 位相スペクトラムを計算
phase_spectrum = np.angle(fft_result)
# 正の周波数のみ取得(実信号の場合、負の周波数は冗長)
positive_freq_mask = frequencies >= 0
frequencies_positive = frequencies[positive_freq_mask]
amplitude_positive = amplitude_spectrum[positive_freq_mask]
phase_positive = phase_spectrum[positive_freq_mask]
# 片側振幅スペクトラムに変換(DC成分以外は2倍)
amplitude_single_sided = amplitude_positive * 2 / N
amplitude_single_sided[0] = amplitude_positive[0] / N # DC成分のみ2倍しない
return frequencies_positive, amplitude_single_sided, phase_positive, fft_result
def plot_fftResult(t, t_short, mixed_signal, frequency, amplitude, phase):
"""FFT結果を美しく可視化"""
fig, axes = plt.subplots(3, 1, figsize=(14, 16), constrained_layout=True)
# 上段:時間領域
time_mask = t <= t_short
axes[0].plot(t[time_mask], mixed_signal[time_mask], 'navy', linewidth=2)
axes[0].set_title('Time Domain Signal (Test Data)', fontsize=14, fontweight='bold', pad=20)
axes[0].set_xlabel('Time [sec]', labelpad=15)
axes[0].set_ylabel('Amplitude')
axes[0].set_xlim(0, t_short)
axes[0].grid(True, alpha=0.3)
# 中段:周波数領域(振幅)
axes[1].plot(frequency, amplitude, 'crimson', linewidth=2)
axes[1].set_title('Frequency Domain Signal (FFT Amplitude)', fontsize=14, fontweight='bold', pad=20)
axes[1].set_xlabel('Frequency [Hz]', labelpad=15)
axes[1].set_ylabel('Amplitude')
axes[1].set_xlim(0, frequency[-1])
axes[1].grid(True, alpha=0.3)
# 下段:周波数領域(位相)
amp_threshold = np.max(amplitude) * 0.05 #振幅ほぼ0の周波数をマスク
phase_mask = amplitude > amp_threshold
axes[2].plot(frequency[phase_mask], phase[phase_mask], 'darkgreen', marker='o', linestyle='None')
axes[2].set_title('Frequency Domain Signal (FFT Phase)', fontsize=14, fontweight='bold', pad=20)
axes[2].set_xlabel('Frequency [Hz]', labelpad=15)
axes[2].set_ylabel('Phase [rad]')
axes[2].set_xlim(0, frequency[-1])
axes[2].set_ylim(-np.pi, np.pi)
axes[2].set_yticks([-np.pi, -np.pi/2, 0, np.pi/2, np.pi])
axes[2].set_yticklabels([r'$-\pi$', r'$-\pi/2$', '0', r'$\pi/2$', r'$\pi$'])
axes[2].grid(True, alpha=0.3, which='both', axis='y')
plt.show()次回予告
次回はFFTにおけるノイズの影響を見ていこうと思います。





コメント