【第2回】
前回の実装の確認編
本記事では、以前の記事でFFT解析の概要を説明するのに使用したpython実装コードの詳細を説明します。以前の記事をまだ読んでいない方は、以前の記事に軽く目を通してからこの記事を読むことをお勧めします。以前の記事はこちら(Pythonで学習するFFT解析➀)。本記事を読むことで、FFT解析の基礎的なpython実装の方法や、FFTを実際に実施する時に注意すべき点がわかります。
※pythonの文法や基本的な使い方に関しては説明しません。
前回のおさらい
FFT解析の実施内容
前回は以下の式で表されるy(t)を、1000Hzで2秒間サンプリングしたデータに対して、FFT解析を実施しました。
\[y(t) = a_1 \sin(\omega_1 t) + a_2 \sin(\omega_2 t) + a_3 \sin(\omega_3 t)\]ただし、
\[\begin{array}{ll}
a_1 = 3 & :周波数\omega_1の振幅 [\;\;] \\
\omega_1 = 2\pi \times 10 & :10\rm{Hz}の角周波数 \rm{ [rad/s] } \\
a_2 = 1.5 & :周波数\omega_2の振幅 [\;\;] \\
\omega_2 = 2\pi \times 30 & :30\rm{Hz}の角周波数 \rm{ [rad/s] } \\
a_3 = 0.8 & :周波数\omega_3の振幅 [\;\;] \\
\omega_3 = 2\pi \times 60 & :60\rm{Hz}の角周波数 \rm{ [rad/s] } \\
\end{array}
\]
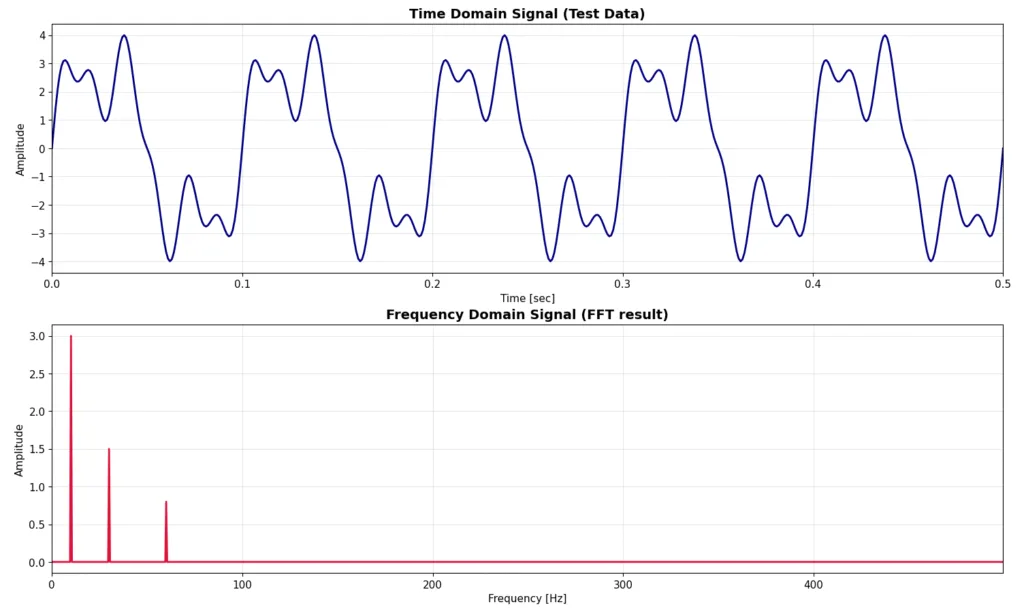
このy(t)を、見やすくするために最初の0.5秒間だけをプロットしたものが、下図の青のプロットです。そしてこのy(t)(正確にはy(t)をサンプリングした離散信号y[k])をFFT解析した結果が、下図の赤のプロットになります。時間領域の信号から周波数領域の信号へと変換がこれでできたというのが、前回説明したところです。
Python実装コードの全体
上記のFFT解析を実施するために使用したPythonの実装コードが以下になります。いったん全体像を改めて示しておきます。
メインプログラム(main.py)
メインプログラムはこちらです。メインプログラムが煩雑になるのを防ぐため、機能ごとに関数化して、FFT_libというファイルにまとめ、それをインポートする形としています。
import numpy as np
import FFT_lib as fft
# サンプリング設定
sampling_rate = 1000 # 1000Hz(1秒に1000回測定)
duration = 2.0 # 2秒間
N = int(sampling_rate * duration) # 総サンプル数
# 時間軸を作成
t = np.linspace(0, duration, N, endpoint=False)
# サンプルデータの周波数と振幅を設定
freq1, freq2, freq3 = 10, 30, 60 # Hz
amp1, amp2, amp3 = 3.0, 1.5, 0.8 # 振幅
# 3つの周波数が混合した信号を生成
signal1, signal2, signal3, mixed_signal = fft.generate_testData(t, freq1, freq2, freq3, amp1, amp2, amp3)
print(f"テストデータが作成されました:y(t) = {amp1}*sin(2π{freq1}t) + {amp2}*sin(2π{freq2}t) + {amp3}*sin(2π{freq3}t)")
# 生成した信号をプロット
t_short = 0.5 # 最初の0.5秒だけ表示
fft.plot_testData(t, 0.5, signal1, signal2, signal3, mixed_signal)
print("時間領域での信号をプロットしました。")
# FFT解析を実行
frequency, amplitude, fft_result = fft.execute_fft(mixed_signal, sampling_rate)
print("FFT解析を実行しました。")
print(f"周波数分解能: {frequency[1] - frequency[0]:.2f} Hz")
print(f"最大周波数: {frequency[-1]:.0f} Hz (ナイキスト周波数)")
# FFT解析の結果をプロット
fft.plot_fftResult(t, t_short, mixed_signal, frequency, amplitude)
関数ファイル(FFT_lib.py)
こちらは関数ファイルです。メインプログラムに使用される機能を関数化してまとめています。
import numpy as np
import matplotlib.pyplot as plt
from scipy.fft import fft, fftfreq
# グラフを美しくする設定
plt.rcParams['figure.figsize'] = (12, 8)
plt.rcParams['font.size'] = 11
# 3つの周波数が混合した信号を生成
def generate_testData(t,freq1,freq2,freq3,amp1,amp2,amp3):
"""3つの周波数が混合した信号を生成
Takes :
t: 時間軸 [sec]
freq1, freq2, freq3: 周波数1, 2, 3 [Hz]
amp1, amp2, amp3: 振幅1, 2, 3 [ ]
Returns:
signal1, signal2, signal3: 個別の正弦波信号 [ ]
mixed_signal: 3つの信号を混合したもの [ ]
"""
signal1 = amp1 * np.sin(2 * np.pi * freq1 * t)
signal2 = amp2 * np.sin(2 * np.pi * freq2 * t)
signal3 = amp3 * np.sin(2 * np.pi * freq3 * t)
# 3つの信号を混合
mixed_signal = signal1 + signal2 + signal3
return signal1, signal2, signal3, mixed_signal
def plot_testData(t, t_short, signal1, signal2, signal3, mixed_signal):
"""時間域での信号をプロット
Takes : t: 時間軸
t_short: 最初の何秒間を表示するか
signal1, signal2, signal3: 個別の正弦波信号
mixed: 3つの信号を混合したもの
Returns: None
"""
fig, axes = plt.subplots(2, 2, figsize=(15, 10))
mask = t <= t_short
t_short_list = t[mask]
# 縦軸範囲を全プロットで統一
y_min = min(signal1[mask].min(), signal2[mask].min(), signal3[mask].min(), mixed_signal[mask].min())
y_max = max(signal1[mask].max(), signal2[mask].max(), signal3[mask].max(), mixed_signal[mask].max())
# 個別信号
axes[0, 0].plot(t_short_list, signal1[mask], 'b-', linewidth=2, label='10Hz')
axes[0, 0].set_title(r'$y_1 = a_1 \sin(\omega_1 t)$', fontweight='bold')
axes[0, 0].grid(True, alpha=0.3)
axes[0, 0].set_ylabel('amplitude')
axes[0, 0].set_xlim(0, t_short)
axes[0, 0].set_ylim(y_min, y_max)
axes[0, 1].plot(t_short_list, signal2[mask], 'g-', linewidth=2, label='30Hz')
axes[0, 1].set_title(r'$y_2 = a_2 \sin(\omega_2 t)$', fontweight='bold')
axes[0, 1].grid(True, alpha=0.3)
axes[0, 1].set_xlim(0, t_short)
axes[0, 1].set_ylim(y_min, y_max)
axes[1, 0].plot(t_short_list, signal3[mask], 'r-', linewidth=2, label='60Hz')
axes[1, 0].set_title(r'$y_3 = a_3 \sin(\omega_3 t)$', fontweight='bold')
axes[1, 0].grid(True, alpha=0.3)
axes[1, 0].set_ylabel('amplitude')
axes[1, 0].set_xlim(0, t_short)
axes[1, 0].set_ylim(y_min, y_max)
# 混合信号
axes[1, 1].plot(t_short_list, mixed_signal[mask], 'purple', linewidth=2)
axes[1, 1].set_title(r'$y = a_1 \sin(\omega_1 t) + a_2 \sin(\omega_2 t) + a_3 \sin(\omega_3 t)$', fontweight='bold')
axes[1, 1].grid(True, alpha=0.3)
axes[1, 1].set_xlim(0, t_short)
axes[1, 1].set_ylim(y_min, y_max)
plt.tight_layout()
plt.show()
def execute_fft(mixed_signal, sampling_rate):
"""信号にFFTを適用して周波数解析
Takes : signal: 入力信号 [ ]
sampling_rate: サンプリング周波数 [Hz]
Returns: frequencies_positive: 正の周波数成分 [Hz]
amplitude_single_sided: 片側振幅スペクトラム [ ]
fft_result: FFTの複素数結果 [ ]
"""
N = len(mixed_signal)
# FFT実行
fft_result = fft(mixed_signal)
# 周波数軸を作成
frequencies = fftfreq(N, 1 / sampling_rate)
# 振幅スペクトラムを計算(複素数の絶対値)
amplitude_spectrum = np.abs(fft_result)
# 正の周波数のみ取得(実信号の場合、負の周波数は冗長)
positive_freq_mask = frequencies >= 0 # DC成分(0Hz)も含む
frequencies_positive = frequencies[positive_freq_mask]
amplitude_positive = amplitude_spectrum[positive_freq_mask]
# 片側振幅スペクトラムに変換(DC成分以外は2倍)
amplitude_single_sided = amplitude_positive * 2 / N
amplitude_single_sided[0] = amplitude_positive[0] / N # DC成分のみ2倍しない
return frequencies_positive, amplitude_single_sided, fft_result
def plot_fftResult(t, t_short, mixed_signal, frequency, amplitude):
"""FFT結果を美しく可視化(片側振幅スペクトラム)"""
fig, (ax1, ax2) = plt.subplots(2, 1, figsize=(14, 10))
# 上段:時間領域
time_mask = t <= t_short
ax1.plot(t[time_mask], mixed_signal[time_mask], 'navy', linewidth=2)
ax1.set_title('Time Domain Signal (Test Data)', fontsize=14,fontweight='bold')
ax1.set_xlabel('Time [sec]')
ax1.set_ylabel('Amplitude')
ax1.set_xlim(0, t_short)
ax1.grid(True, alpha=0.3)
# 下段:周波数領域
ax2.plot(frequency, amplitude, 'crimson', linewidth=2)
ax2.set_title('Frequency Domain Signal (FFT result)', fontsize=14, fontweight='bold')
ax2.set_xlabel('Frequency [Hz]')
ax2.set_ylabel('Amplitude')
ax2.set_xlim(0, frequency[-1])
ax2.grid(True, alpha=0.3)
plt.tight_layout()
plt.show()Python実装コードの説明
今回のmain.pyは大きく分けて5つの部分に構成を分けることができます。
- 変数(サンプリング、周波数等など)の設定
- テストデータの作成(時間領域の信号)
- テストデータの可視化
- FFTの実施(時間領域信号→周波数領域信号)
- FFT解析の可視化
以下にこれらを1つ1つmain.pyのプログラムの順番に説明していきます。
変数(サンプリング、周波数等など)の設定
これはmain.pyの中で以下の部分が該当します。特に特筆して説明が必要な部分はないとは思います。sampling_rateがy(t)をサンプリングする周波数の1000Hz、durationがサンプリング時間の2秒です。Nがsampling_rate×durationで、データ点数です。y(t)のデータを作成するために、a1,a2,a3,w1,w2,w3,をそれぞれ設定している程度です。
ここで強いて1つだけポイントがあるとすれば、7行目の時間軸tを作成する際のnp.linspaceで、endpoint=Falseとしている点です。
# サンプリング設定
sampling_rate = 1000 # 1000Hz(1秒に1000回測定)
duration = 2.0 # 2秒間
N = int(sampling_rate * duration) # 総サンプル数
# 時間軸を作成
t = np.linspace(0, duration, N, endpoint=False)
# サンプルデータの周波数と振幅を設定
freq1, freq2, freq3 = 10, 30, 60 # Hz
amp1, amp2, amp3 = 3.0, 1.5, 0.8 # 振幅Numpyの公式ドキュメント(こちら)を確認すると、linspaceは以下のように説明されています。
numpy.linspace(start, stop, num=50, endpoint=True, retstep=False, dtype=None, axis=0, *, device=None)endpoint: bool, optional
If True, stop is the last sample. Otherwise, it is not included. Default is True.
このendpoint=True (or False)が意味するところは、引数のstartをデータの1つ目とし、stopまで、num個のデータを作った際に、最後のnum番目のデータをstopの値そのものにするか、stopの値は含めないかを選択できるということです。今回私の実装ではあえてこの部分をendpoint = Falseにしています。理由は2つあります。
1つ目の理由はシンプルで、1000Hzつまり、サンプリング時間間隔をぴったり0.001秒にするためです。endpoint=Trueにしてしまうと、0から2を含めてN(2000)個のデータにする必要があり、dtが0.001より大きくなってしまうためです。
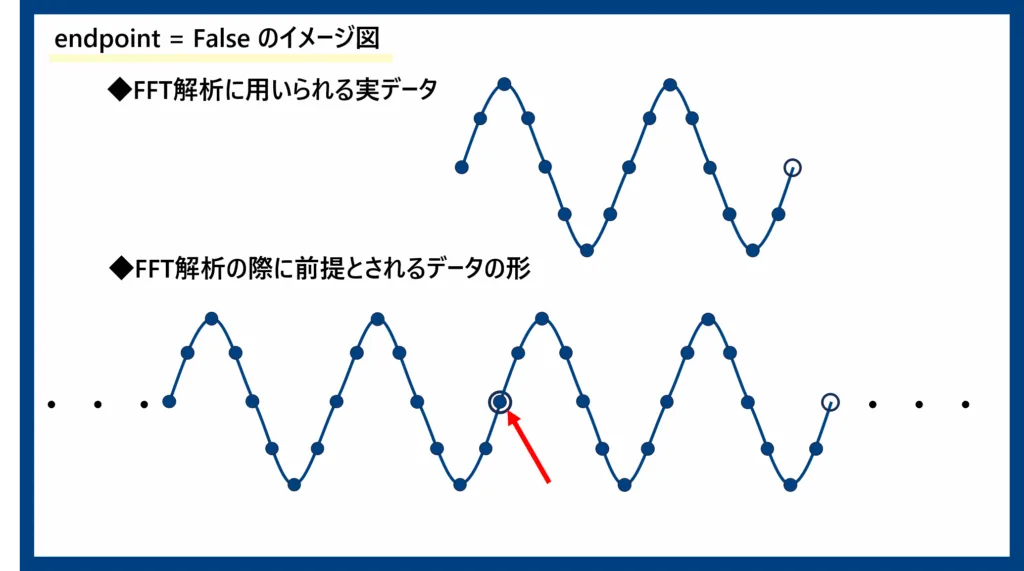
2つ目の理由は、少し難しいので今回はイメージだけ説明します(詳細はスペクトル漏れの記事を書く際に説明します)。FFT(及びDFT)は解析対象となるデータが無限に繰り返されることを前提とした解析です。今回のy(t)に含まれる周波数はすべて10, 30, 60Hzと、2秒間の中に整数回分の繰り返しがぴったり完了するような信号の重ね合わせです。つまり、endpoint=Falseにすることで、信号を繰り返した際にきれいに周期性が保存されるのです。
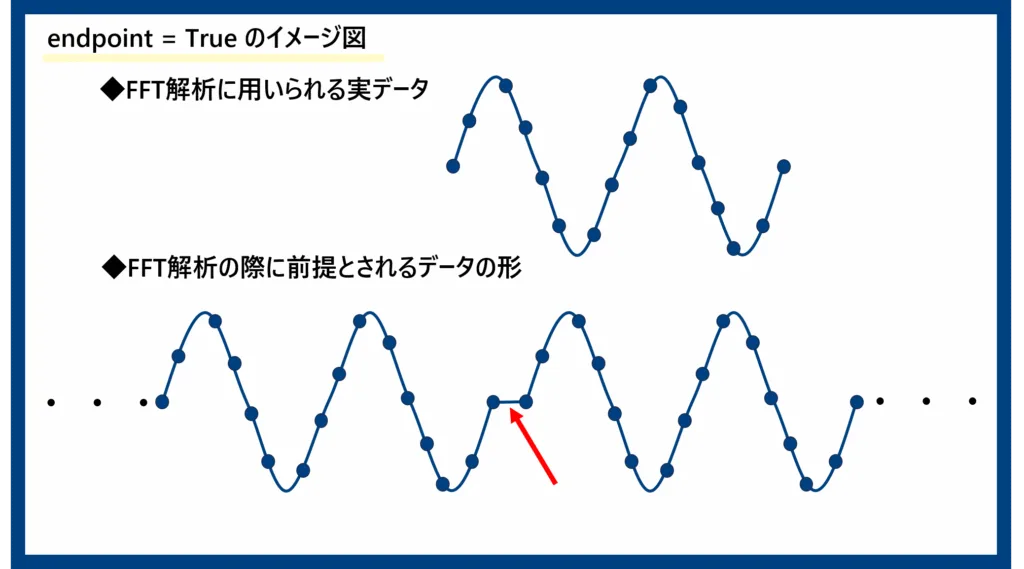
一方で、endpoint=Trueにしてしまうと、FFTを実行する時に前提するデータが1周期+1点分のデータとなってしまいます。これをそのままFFT解析してしまうと下図のように前提とするデータの周期性が崩れてしまい、FFT解析の結果に、本来含まれていないはずの周波数が出てきてしまうことに繋がります。これは信号の不連続によるスペクトル漏れ(Spectral leakage)などとも呼ばれる現象です。
今回はこれ以上のスペクトル漏れの話は本筋から外れてしまうので、この辺までとします。
テストデータの作成(時間領域の信号)
次にテストデータy(t)を作成する部分を説明します。main.pyの中でテストデータを作っているのは以下の部分です。ほとんどがgenerate_testData(*)の中でやってしまっているので、メインプログラムの中ではほんの1行でテストデータがつくられています 。
# 3つの周波数が混合した信号を生成
signal1, signal2, signal3, mixed_signal = fft.generate_testData(t, freq1, freq2, freq3, amp1, amp2, amp3)
print(f"テストデータが作成されました:y(t) = {amp1}*sin(2π{freq1}t) + {amp2}*sin(2π{freq2}t) + {amp3}*sin(2π{freq3}t)")fft.generate_testData(*)という部分に関しては、FFT_lib.pyから関数を呼びだしています。その部分は以下になります。
# 3つの周波数が混合した信号を生成
def generate_testData(t,freq1,freq2,freq3,amp1,amp2,amp3):
"""3つの周波数が混合した信号を生成
Takes :
t: 時間軸 [sec]
freq1, freq2, freq3: 周波数1, 2, 3 [Hz]
amp1, amp2, amp3: 振幅1, 2, 3 [ ]
Returns:
signal1, signal2, signal3: 個別の正弦波信号 [ ]
mixed_signal: 3つの信号を混合したもの [ ]
"""
signal1 = amp1 * np.sin(2 * np.pi * freq1 * t)
signal2 = amp2 * np.sin(2 * np.pi * freq2 * t)
signal3 = amp3 * np.sin(2 * np.pi * freq3 * t)
# 3つの信号を混合
mixed_signal = signal1 + signal2 + signal3
return signal1, signal2, signal3, mixed_signalこのgenerate_testDataは引数に、時間軸(N×1)と、3つの周波数と、3つの振幅をとり、戻り値として、a1*sin(w1t)、a2*sin(w2t)、a3*sin(w3t)と、その3つの足し合わせを返す関数です。戻り値は、すべてN×1の次元です。
※singal1, signal2, signal3は、重ね合わせの元の信号を視覚化し、説明するために作った信号なので、実際のFFT解析においては特に重要ではありません。FFT解析にはmixed_signalが使用されます。
print(**)部を実行すると、コンソールに以下が表示されるようになっています。このように各機能の終わりに、期待結果などコメントを表示するようにしていると、デバッグがしやすいのでお勧めです。
テストデータが作成されました:y(t) = 3.0sin(2π10t) + 1.5sin(2π30t) + 0.8*sin(2π60t)
テストデータの可視化
次は生成したテストデータをプロットします。main.pyの中の以下の部分がそれに該当します。
# 生成した信号をプロット
t_short = 0.5 # 最初の0.5秒だけ表示
fft.plot_testData(t, 0.5, signal1, signal2, signal3, mixed_signal)
print("時間領域での信号をプロットしました。")こちらも、plotの詳細に関してはfft.plot_testData(**)の中でやってしまっています。このplot_testData(**)に関しては特に説明する箇所もないのでスキップします。
FFTの実施(時間領域信号→周波数領域信号)
次はいよいよFFTの実行です。FFTを実行しているのは、メインプログラムで言うと以下の部分が該当します。
# FFT解析を実行
frequency, amplitude, fft_result = fft.execute_fft(mixed_signal, sampling_rate)
print("FFT解析を実行しました。")
print(f"周波数分解能: {frequency[1] - frequency[0]:.2f} Hz")
print(f"最大周波数: {frequency[-1]:.0f} Hz (ナイキスト周波数)")この中の、fft.execute_fft(**)という部分が実質FFTを実行している部分で、この中身はFFT_lib.pyの以下の部分が該当します。
def execute_fft(mixed_signal, sampling_rate):
"""信号にFFTを適用して周波数解析
Takes : signal: 入力信号 [ ]
sampling_rate: サンプリング周波数 [Hz]
Returns: frequencies_positive: 正の周波数成分 [Hz]
amplitude_single_sided: 片側振幅スペクトラム [ ]
fft_result: FFTの複素数結果 [ ]
"""
N = len(mixed_signal)
# FFT実行
fft_result = fft(mixed_signal)
# 周波数軸を作成
frequencies = fftfreq(N, 1 / sampling_rate)
# 振幅スペクトラムを計算(複素数の絶対値)
amplitude_spectrum = np.abs(fft_result)
# 正の周波数のみ取得(実信号の場合、負の周波数は冗長)
positive_freq_mask = frequencies >= 0 # DC成分(0Hz)も含む
frequencies_positive = frequencies[positive_freq_mask]
amplitude_positive = amplitude_spectrum[positive_freq_mask]
# 片側振幅スペクトラムに変換(DC成分以外は2倍)
amplitude_single_sided = amplitude_positive * 2 / N
amplitude_single_sided[0] = amplitude_positive[0] / N # DC成分のみ2倍しない
return frequencies_positive, amplitude_single_sided, fft_result
まず12行目のfft_result = fft(mixed_signal)の部分を説明します。ここで先ほど生成した、時間領域のデータをfft(*)の引数として渡してあげることでFFTが実行された値が戻り値として取得できます。fft(*)という関数は、FFT_lib.pyの最初にimportしたscipy.fftの中に入っている関数(method)になります。scipy.fft.fft(*)の公式ドキュメント(こちら)を確認するると、scipy.fft.fft(*)の使い方が以下のように説明されています。以下、公式ドキュメントの一部抜粋です。
fft(x, n=None, axis=-1, norm=None, overwrite_x=False, workers=None, *, plan=None)Compute the 1-D discrete Fourier Transform.
This function computes the 1-D n-point discrete Fourier Transform (DFT) with the efficient Fast Fourier Transform (FFT) algorithm
Returns:
out:complex ndarray
引数が色々あるように見えますが、x以外の引数はすべてoptionalなので指定しなくて大丈夫です。今回はこのxのところにmixed_signalが入ってるということになります。そして、fft(mixed_signal)の戻り値として、complex ndarray、つまり複素数のndarrayが返ってくるというものです。今回の場合は以下のようなN=2000のndarrayがfft_resultに格納されるはずです。
| 0 | [4.084e-13, -0.000e+00j] |
| 1 | [6.527e-14, +2.473e-13j] |
| : | : |
| 1999 | [6.527e-14, +2.473e-13j] |
この値が、以下のDFTの式で計算されたX[k]の値に対応します(計算の処理はFFTとして処理されている)。このX[k]は周波数スペクトルや、複素スペクトルと呼ばれます。
\[X[k] = \sum_{n=0}^{N-1} x[n] \cdot \exp\left(-j\frac{2\pi kn}{N}\right)\]次に15行目のfrequencies = fftfreq(**)について説明します。ここは、先ほど得られたfft_resultの周波数スペクトルに対応する周波数軸を作成しています。frequenciesには、fft_resultと同じデータ数のndarrayが格納され、fft_result[k]に対応する周波数が、frequencies[k]に格納されています。
一応、scipy.fft.fftfreq(*)の公式ドキュメント(こちら)も確認しておきましょう。以下は公式ドキュメントからの一部抜粋です。
fftfreq(n, d=1.0, *, xp=None, device=None)Parameters:
n int:Window length
d scalar, optional, :Sample spacing (inverse of the sampling rate). Defaults to 1.
Returns:
f ndarray:Array of length n containing the sample frequencies.
fftfreqにn(データ点数)とd(サンプリング間隔[sec])を渡してあげると、n次元のndarrayとして周波数の軸が戻り値として帰ってくるというわけです。今回の場合はデータ点数はN=2000で、サンプリング周波数はsampling_rate =1000Hzです。つまりnにはN(2000)を渡し、dはoptionalとなっていますが、何も指定しないとデフォルトの設定は1秒となってしまうので、dには1/sampling_rate = 0.001を渡してあげると、今回の例の周波数軸が作成されます。
次に18行目から27行目までの部分を説明します。まず18行目ですが、FFTの結果得られるものは、先ほど見たように複素スペクトルで、このままでは振幅が実際どの程度の大きさなのかわかりません。np.abs(fft_result)で絶対値を撮ることで振幅スペクトルを取得しています。先ほどのX[k]の絶対値を取得しています。
\[|X[k]|\]ただし、このX[k]の絶対値を取っただけでは実際の振幅そのものは得られません。ここから実際の各周波数の振幅を得るためには以下の式を計算する必要があります。
\[\begin{array}{ll}
A_0 = \frac{1}{N}\left|X[0]\right|& :DC成分(k=0 の 0 \rm{Hz}部分)\\
A = \frac{2}{N} \left| X[k] \right|& :k\neq0(0 \rm{Hz}以外の部分)\\
\end{array}
\]
まずは、振幅スペクトル|X[k]|をデータ点数Nで割ります。これは、DFTの計算が「離散和」であり、本来のフーリエ変換は「積分」であるため、その差を補正するためにデータ点数Nで割る必要があるのです。連続時間の積分だとx(t)にdtという微小時間をかけていますが、DFTの計算にはこのdtに対応するものがなく、データ点数が多くなればなるほどその差が積みあがります。そのためDFTの結果に対して、データ点数Nで割ることで、連続時間のフーリエ変換と同じ次元の振幅が得られるというわけです。そして、2をかける(DC成分以外)のは、FFTの結果は、k=0,1,…,N-1のN個が得られますが、実数信号の場合はスペクトルが 正周波数と負周波数に対して対称になり、振幅が両側(正側・負側)に分散して表現されるため、正の周波数側だけで表現したいときには 2倍する必要があるためです。ただし、DC成分(k=0)は片側にしか現れないので 2倍しません。(※正確にはナイキスト周波数の部分もデータ点数が偶数点数の時は片側にしか現れないので2倍しないのですが、今回はその部分の説明は省略します)
この計算をして、最終得られたものが、正の周波数軸を格納したfrequencies_positiveと、正の周波数の振幅を格納したamplitude_single_sidedです。この2つがFFT解析においてほしい情報になります。
ちなみにこの部分のprint(*)部は以下のようにコンソールに表示されます。ナイキスト周波数と周波数分解能に関しては後述します。
FFT解析を実行しました。
周波数分解能: 0.50 Hz
最大周波数: 500 Hz (ナイキスト周波数)
FFT解析の可視化
最後に、先ほど得られた周波数軸と、振幅を可視化します。メインプログラムの中では以下の部分です。こちらも特に説明が必要な部分はないと思いますので、説明はスキップします。
# FFT解析の結果をプロット
fft.plot_fftResult(t, t_short, mixed_signal, frequency, amplitude)以上で、y(t)を1000Hzでサンプリングした2秒間の信号をFFT解析する、という作業のすべての説明が完了しました。
ナイキスト周波数と周波数分解能
FFTを実施する際に、知っておく必要があることとして「ナイキスト周波数」と「周波数分解能」があります。特にナイキスト周波数は知っておかないと、実際にやりたい周波数解析に対してセンサの適切な選定ができないことになってしまうので、非常に重要な概念です。
ナイキスト周波数
ナイキスト周波数とは、時間領域信号のサンプリング周波数fsに対し、その半分の周波数のことを差します。
\[f_{\rm{Nyquist}}=\frac{f_s}{2}\]なぜこのナイキスト周波数が大切かというと、FFT解析において解析できる限界の周波数がナイキスト周波数だからです。今回の場合はサンプリング周波数は1000Hzなので、500Hz以上の周波数(例えば600Hz)がもしy(t)に含まれていても、それはFFT解析をしても、600Hzの信号としては出てこないのです。今回の私のFFTの結果のプロットを見てもらっても500Hzまでしかプロットしていないのがわかると思います。(500Hz以上をプロットしても500Hzの軸を中心に折り返しただけのプロットになるだけなので意味がないのです)。
ではもし元の信号y(t)にナイキスト周波数以上の周波数が含まれていたらどうなるのでしょうか?
それは、エイリアシングと呼ばれる現象が発生し、サンプリング周波数で折り返した周波数に偽物のピークとして表れてしまうのです。式で書くと以下になります。
\begin{array}{ll}
f_{\rm{fake}}=|f – mf_s| &:mは自然数
\end{array}
\]
ただしmはf_fakeがナイキスト周波数より小さくなるように選ばれます。
例えばy(t)のw3が60Hzでなくて、600Hzだった場合、
\[f_{\rm{fake}}=|600 -1\cdot 1000| = 400\]となり、400 [Hz]のところに偽のピークがたちます。
実際に、今回説明したpythonコードのw3の周波数を600Hzに変えて実行した結果を表示すると以下のようになります。60Hzがなくなって、600Hzが追加されたことで元の時間領域信号も、かなりギザギザしていますね。そして、FFTの結果もエイリアシングの影響で400Hzに偽のピークがたっていることがわかります。FFTの結果だけみると、元信号に含まれているのが400Hzなのか600Hzなのか、はたまた1400Hzなのか、全く区別はつきません。これを正しく600Hzと判断できるためには元データの形状を見る必要があります。このような現象が発生するため、FFT使用者は偽のピークに騙されないための、十分な背景知識が必要になるのです。一応、対策としてはFFT解析を実施する際にアンチエイリアシングフィルタを入れるということもできますが、それを実施してもナイキスト周波数以上の周波数が解析できないことに変わりはありません。
# サンプルデータの周波数と振幅を設定
freq1, freq2, freq3 = 10, 30, 600 # Hz
amp1, amp2, amp3 = 3.0, 1.5, 0.8 # 振幅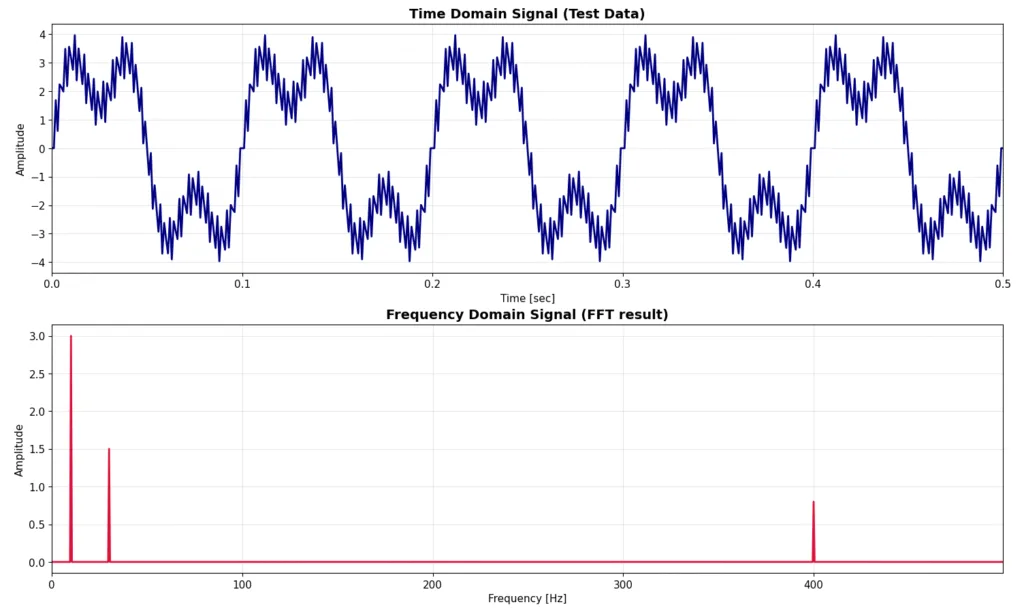
上記からわかることとして覚えておくべきことは、ナイキスト周波数を上げるためにはサンプリング周波数を上げる必要が有るということです。つまり実用途を考えると、サンプリング周波数が高いセンサを使えば使うほど、高周波まで周波数解析ができるということです。逆に言うと、どの周波数帯域まで解析できるかは、センサのサンプリング周波数によって決まってしまうということです。
周波数分解能
最後にFFTを実施する際の周波数分解能がどのように決まるかを説明します。ここは特にポイントはなく、単純にこうなるというだけです。周波数分解能は以下の式によって決まります。
\[\Delta f = \frac{f_s}{N}\]今回の場合、サンプリング周波数は1000Hzで、データはN=2000なので、周波数分解能Δfは0.5 [Hz]ということになります。また、サンプリング時間Tが
\[T = \frac{N}{f_s}\]という式で表されることを勘案すると、周波数分解能は以下の式でも表すことができます。
\[\Delta f = \frac{1}{T}\]サンプリング時間Tは今回2秒だったので、Δfは0.5 [Hz]となりますね。
つまり周波数分解能はデータを長く取ればとるだけ上がるということになります。(センサに依存しない)
次回予告
次回は、FFT解析における位相情報と、今回あまり説明しなかったDC成分について説明したいとおもいます。
今回は内容が盛りだくさんだったので、次回はもう少しさらっと説明しようと思います。





コメント